36.3. Оценка точного значения измеряемой величины
Пусть в итоге п независимых измерений некоторой величины X получены следующие результаты:
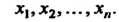 (36.13)
(36.13)
Будем предполагать, что эти результаты свободны от грубых и систематических ошибок (неверные результаты отброшены, на систематические ошибки введены поправки). Оценить точное значение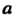 Измеряемой величины - значит:
Измеряемой величины - значит:
А) определить функцию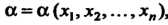 , которая обеспечивает достаточно близкое приближение к значению
, которая обеспечивает достаточно близкое приближение к значению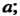
Б) указать границы интервала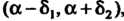 , который с заданной вероятностью у покрывает истинное значение
, который с заданной вероятностью у покрывает истинное значение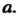
Среднее арифметическое значение (среднее значение)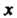 Результатов (36.13), среднее квадратическое отклонение
Результатов (36.13), среднее квадратическое отклонение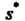 Этих результатов от их среднего значения х и эмпирический стандарт
Этих результатов от их среднего значения х и эмпирический стандарт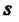 Определяются соответственно формулами:
Определяются соответственно формулами:
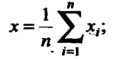 (36.14)
(36.14)
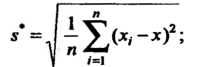 (36.15)
(36.15)
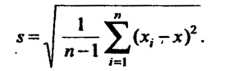 (36.16)
(36.16)
Если все измерения проведены с одинаковой точностью, то в качестве опенки точного значения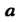 Измеряемой величины принимают среднее арифметическое значений результатов (36.13):
Измеряемой величины принимают среднее арифметическое значений результатов (36.13):
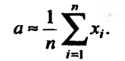 (36.17)
(36.17)
Эта оценка является несмещенной и состоятельной. Введенная оценка оказывается и эффективной при дополнительном предположении о том, что случайные ошибки измерений подчинены нормальному закону распределения. Это предположение имеется в виду и в дальнейшем. Оценка (36.17) относится к числу точечных оценок. Симметрические доверительные оценки имеют вид
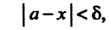 Или
Или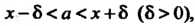 (36.18)
(36.18)
Где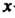 - среднее значение, определяемое формулой (36.14). Величина
- среднее значение, определяемое формулой (36.14). Величина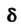 (точность оценки) определяется по заданной доверительной вероятности
(точность оценки) определяется по заданной доверительной вероятности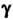 (надежности оценки).
(надежности оценки).
Если известно среднее квадратическое отклонение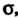 То доверительная оценка
То доверительная оценка
(36.18) имеет вид
Где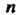 - число измерений, а значение
- число измерений, а значение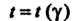 Определяется по заданной довери
Определяется по заданной довери
Тельной вероятности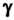 Из условия
Из условия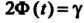 И находится с помощью таблиц. Точ
И находится с помощью таблиц. Точ
Ность оценки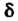 В этом случае выражается формулой
В этом случае выражается формулой
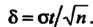 (36.20)
(36.20)
Если средняя квадратическая погрешность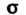 Заранее неизвестна, то вместо нее применяют эмпирический стандарт
Заранее неизвестна, то вместо нее применяют эмпирический стандарт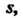 Который служит оценкой параметра
Который служит оценкой параметра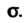 Доверительная оценка (36.18) принимает вид
Доверительная оценка (36.18) принимает вид
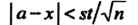 (36.21)
(36.21)
Или
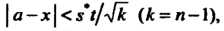 (36.22)
(36.22)
Где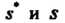 Определяются соответственно формулами (36.15) и (36.16), а множи
Определяются соответственно формулами (36.15) и (36.16), а множи
Тель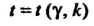 Зависит не только от доверительной вероятности
Зависит не только от доверительной вероятности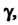 Но и от числа
Но и от числа
Измерений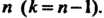 Значения этого множителя определяются по таблицам.
Значения этого множителя определяются по таблицам.
Правило трех сигм представляет собой доверительную оценку
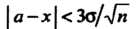 (36.23)
(36.23)
При известной величине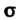 Или доверительную оценку
Или доверительную оценку
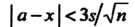 (36.24)
(36.24)
При неизвестной величине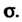 Оценка (36.23) имеет надежность
Оценка (36.23) имеет надежность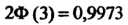 Незави
Незави
Симо от числа измерений. Оценка (36.24) зависит от числа измерений и (зависимость эта устанавливается с помощью соответствующих таблиц).
| < Предыдущая | Следующая > |
|---|