36.2. Доверительный интервал. Доверительная вероятность

Оценка, определяемая одним числом, называется точечной. Оценка, определяемая двумя числами - концами интервалов, называется интервальной.

Доверительной вероятностью (надежностью) оценки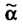Параметра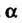Называется вероятность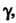С которой осуществляется неравенство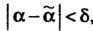, т. е.

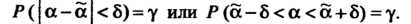
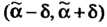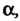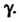Эта формула означает следующее: вероятность того, что интервал заключает в себе (покрывает) неизвестный параметрРавнаИнтервал 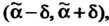Который покрывает неизвестный параметр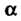С заданной надежностью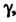Называется доверительным интервалом. Концы доверительного интервала называю т доверительными границами.

Если случайная величина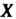Имеет нормальное распределение с заданным средним квадратическим отклонением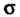И неизвестным математическим ожиданием а, то

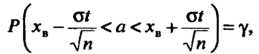(36.10)

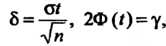(36.11)

Т. е. доверительный интервал

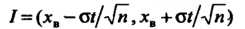(36.12)

Покрывает неизвестный параметр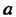С надежностью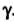. Значение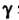Задано заранее; число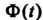Определяется второй из формуя (36.11); значение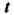Находится с помощью таблиц значений функции Лапласа; точность оценки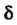Выражается первой из формул (36.11).

Пример 36.2. Найти доверительный интервал для оценки математического ожидания а нормальной случайной величины с надежностью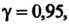Зная выборочную

Среднюю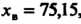, объем выборки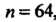, среднее квадратическое отклонение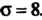

Доверительный интервал определяется формулой (36.12). Чтобы найти концы доверительного интервала, необходимо знать значение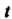(значенияЗада

Ны). Второе из равенств (36.11) примет вид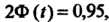Откуда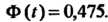По

Таблице значений функции Лапласа находим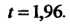Подставляя значения

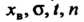В выражения для концов доверительного интервала, получаем

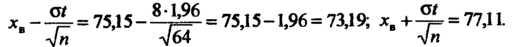
Следовательно,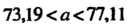, т. е.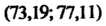— искомый доверительный интервал.

< Предыдущая		Следующая >