38.4. Решение дифференциальных уравнений и их систем

Методы операционного исчисления применяются при интегрировании дифференциальных уравнений и их систем. С помощью этих методов интегрирование некоторых классов линейных дифференциальных уравнений сводится к решению алгебраических уравнений; из алгебраического уравнения находят изображение решения данного уравнения, после чего по изображению восстанавливают само решение.

Пусть требуется найти решение линейного дифференциального уравнения с постоянными коэффициентами

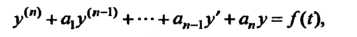(38.26)

Удовлетворяющее нулевым начальным данным

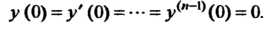(38.27)

Предположим, что искомая функция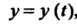, ее производные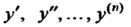

И данная функция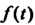Являются оригиналами. Обозначим изображения функций

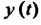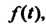ИСоответственно, через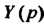И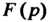Или короче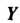И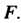Пользуясь

Ими и правилом дифференцирования оригинала (см. формулы (38.8)), находим

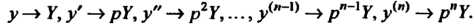(38.28)

Поскольку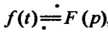, то на основании свойства линейности (см. формулу

(38.6)) получим уравнение в изображениях

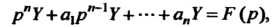(38.29)

Которое соответствует данному дифференциальному уравнению. Из уравнения (38.29) найдем изображение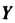Искомого решения

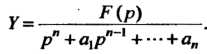(38.30)

Найдя изображение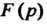Функции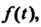Получим изображение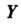И вопрос будет сведен к отысканию соответствующего оригинала, который является решением данного дифференциального уравнения и удовлетворяет нулевым начальным данным.

Таким образом, чтобы решить уравнение (38.26), необходимо знать, как по оригиналу найти изображение и по данному изображению - оригинал.

При интегрировании дифференциальных уравнений находит применение интеграл Дюамеля (см. формулу (38.20)). Пусть необходимо найти решение дифференциального уравнения (38.26), удовлетворяющее условиям (38.27). Запишем дифференциальное уравнение с такой же левой частью и правой частью, равной единице:

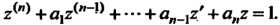(38.31)

Будем искать решение этого уравнения, удовлетворяющее начальным нулевым данным:

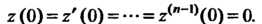(3832)

Обозначим изображение решения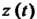Через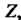Получим уравнение в изображениях

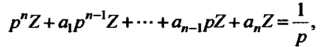(38.33)

Откуда

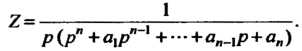(38.34)

Из этого равенства и равенства (38.30) находим, что

Пользуясь интегралом Дюамеля, получаем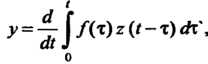

Или

Таким образом, когда известно решение уравнения (38.26) при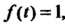Удовлетво

Ряющее нулевым начальным данным, то можно фазу найти в квадратурах решение этого уравнения для любой функцииПри тех же начальных данных.

Замечание 1. Если начальные данные не являются нулевыми, то изображения производных находятся с помощью формул (38.7). Например, если 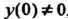, то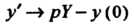И т. д.

Замечание 2. Если за начальный момент взято значени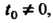еА не

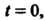То вводят новую переменную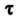По формуле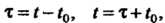Тогда

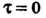При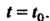

С помощью операционного исчисления можно найти решения систем дифференциальных уравнений с постоянными коэффициентами, а в некоторых случаях

— решения дифференциальных уравнений с переменными коэффициентами, решения дифференциальных уравнений в частных производных.

Пример 38.21. Найти решение уравнения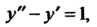Удовлетворяющее

Условиям: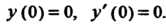

Обозначим через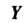Изображение функции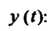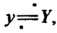Тогда

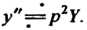Поскольку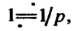То уравнение в изображениях имеет вид

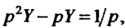Откуда

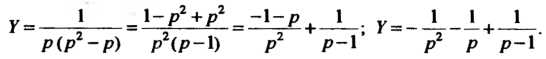
Принимая во внимание формулы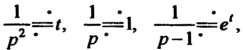Получаем

Искомое решение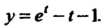Легко проверить, что эта функция удовлетворяет

Данному уравнению и нулевым начальным данным.

Пример 38.22. Найти решение уравнения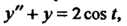Удовлетво

Ряющее условиям: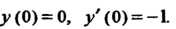

Изображение функции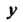Обозначим через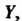А изображения производных найдем с помощью формул (38.7):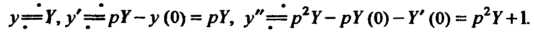

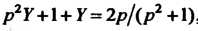, отедца

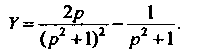
Так как (см. примеры 38.4 и 38.9)

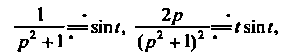
То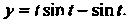Получено решение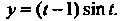

Пример 38.23. Проинтегрировать уравнение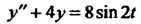При на

Чальных условиях: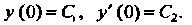

Обозначим через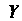Изображение решения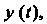А изображения производных

Найдем с помощью формул (38.7):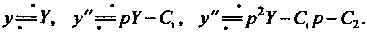

Поскольку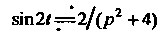(см. пример 38.4), то операторное уравнение

Принимает вид

Откуда

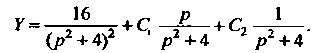
Для двух последних слагаемых имеем:

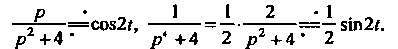
Что касается оригинала для первого слагаемого, то его найдем с помощью формулы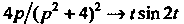(см. пример 38.9) и правила интегрирования ори

Гинала (см. формулу (38.9)) следующим образом: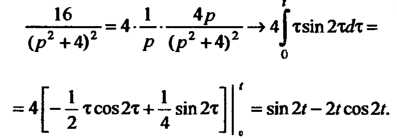

Значит, искомое решение имеет вид 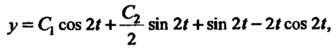 или

Пр и м е р 38.24. Проинтегрировать уравнение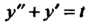При начальных

Данных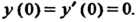

Найдем сначала решение уравнения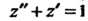При нулевых начальных дан

Ных. Уравнение в изображениях имеет вид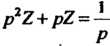, откуда

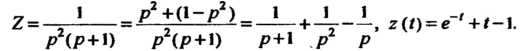
На основании формулы (38.36) получаем

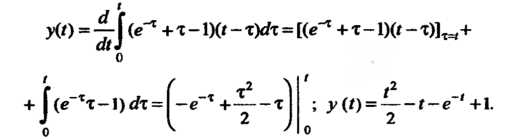
Пример 38.25. Найти решение уравнения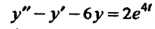, удовле

Творяющее условиям: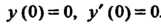

Операторное уравнение в заданном случае принимает вид

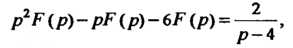
Откуда

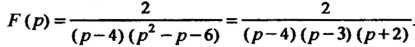
Разлагая эту дробь на элементарные дроби, находим 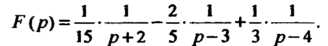 Следовательно, искомое решение определяется формулой

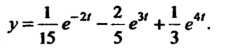
Пример 38.26. Найти решение задачи Коши: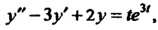

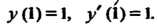
В отличие от предыдущих примеров, здесь за начальный момент взято значени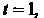еА не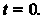Введем новую переменную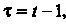Откуда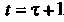. Обозначим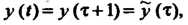Тогда уравнение и начальные данные принимают вид:

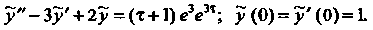Найдем решение этого уравнения:

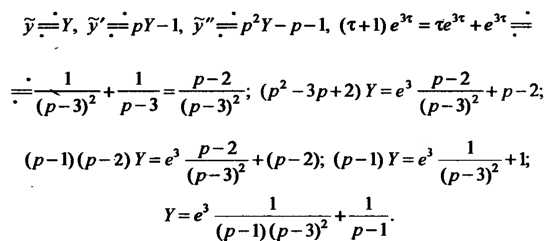
Поскольку

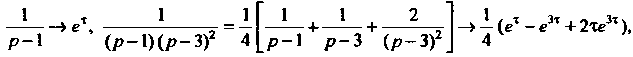
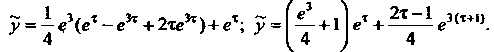
Возвращаясь к переменной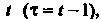Получаем решение исходной задачи Коши

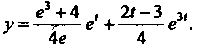
Пр и м е р 38.27. Найти решение уравнения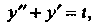Удовлетворяющее

Условиям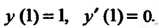

Положим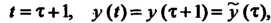Тогда уравнение и начальные

Условия примут вид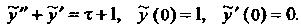Составим оператор

Ное уравнение для этого дифференциального уравнения. Пусть

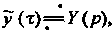Тогда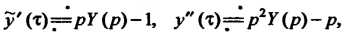Операторное

Уравнение и его решение запишутся так:

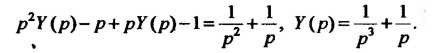
Переходя к оригиналам, получаем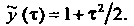Возвращаясь к пере

Менной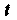(заменив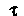На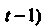, найдем искомое решение исходной задачи Коши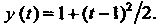

Пр и м е р 38.28. Найдем решение системы дифференциальных уравнений

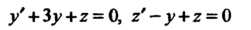
При начальных условиях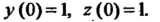

При обозначениях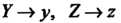Система в изображениях принимает вид

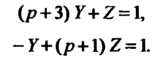
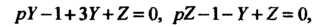
Решение системы получим с помощью формул Крамера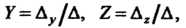 где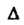— определитель системы,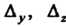— определители, полученные из опреде

Лителей системы заменой коэффициентов при соответствующих неизвестных свободными членами. Поскольку

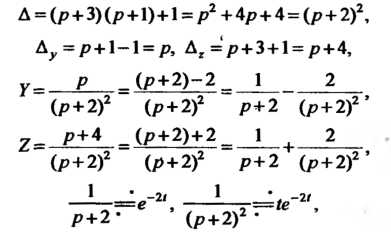
То

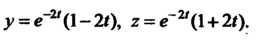
Пр имер 38.29. Найти решение системы

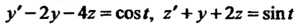
При начальных условиях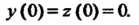

Система в изображениях принимает вид

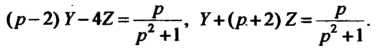
Изображения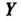И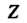Определяем с помощью формул Крамера. Поскольку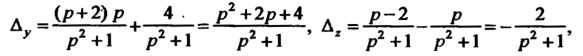  

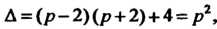
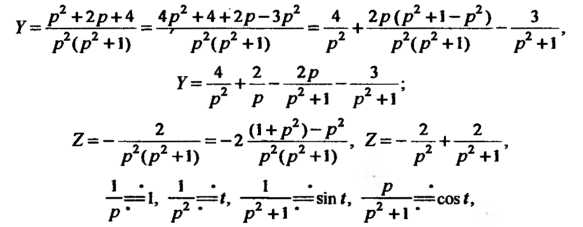
То

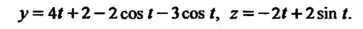
Пример 38.30. Найти решение системы

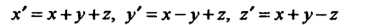
При начальных данных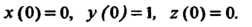

В изображениях система принимает вид

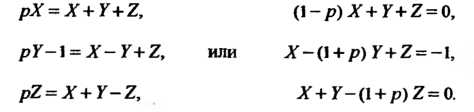
Изображения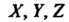Находим с помощью формул Крамера. Поскольку

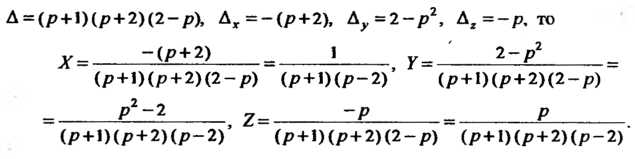
Разлагая полученные дроби на элементарные, найдем, что

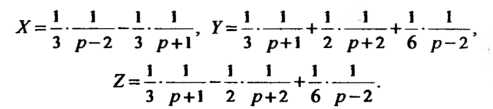
Принимая во внимание равенство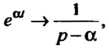Получаем искомое решение системы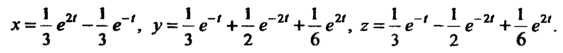

< Предыдущая		Следующая >