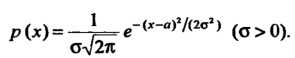35.6. Некоторые законы распределения случайных величин
Пусть производятся испытания, в каждом из которых может появится событие Л. Если вероятность события А в одном испытании не зависит от появления его в любом другом, то испытания называют независимыми относительно события А. Будем считать, что испытания происходят в одинаковых условиях и вероятность появления события А в каждом испытании одна и та же; обозначим эту вероятность через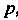 , а через
, а через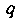
- вероятность появления события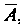 , противоположного событию
, противоположного событию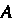
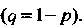
Вероятность того, что в серии из и независимых испытаний событие А появится ровно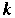 Раз (и не появится
Раз (и не появится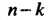 Раз), выражается формулой Бернулли
Раз), выражается формулой Бернулли
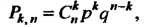 (35.19)
(35.19)
Где
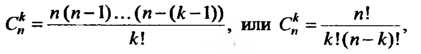
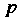 —вероятность события
—вероятность события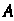 В каждом испытании,
В каждом испытании,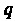 — вероятность события
— вероятность события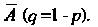 Закон распределения дискретной случайной величины, определяемый формулой Бернулли, называется биноминальным. Биноминальный закон распределения дискретной случайной величины можно представить в виде схемы
Закон распределения дискретной случайной величины, определяемый формулой Бернулли, называется биноминальным. Биноминальный закон распределения дискретной случайной величины можно представить в виде схемы

Для случайной величины, распределенной по биноминальному закону с параметрами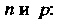
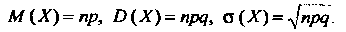
Геометрическим распределением называется распределение дискретной случайной величины X, определяемое формулой
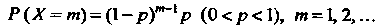
Это название связано с тем, что ряд вероятностей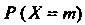 Представляет собой
Представляет собой
Бесконечно убывающую геометрическую прогрессию со знаменателем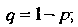 сумма этого ряда равна единице. Для геометрически распределенной случайной величины
сумма этого ряда равна единице. Для геометрически распределенной случайной величины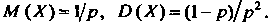
Распределением Пуассона называется распределение дискретной случайной величины, определяемое формулой
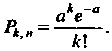
Для случайной величины, распределенной по закону Пуассона, 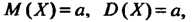 Где
Где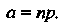
Случайная величина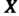 Называется равномерно распределенной на отрезке
Называется равномерно распределенной на отрезке 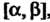 , если плотность распределения вероятностей этой величины постоянна на данном отрезке и равна нулю вне его:
, если плотность распределения вероятностей этой величины постоянна на данном отрезке и равна нулю вне его:
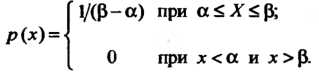
Для случайной величины X, равномерно распределенной на отрезке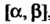 , вероятность попадания в интервал
, вероятность попадания в интервал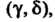 Принадлежащий этому отрезку, пропорциональна длине интервала:
Принадлежащий этому отрезку, пропорциональна длине интервала:
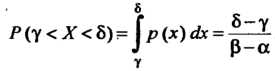
Функция распределения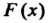 Этой величины имеет виц
Этой величины имеет виц
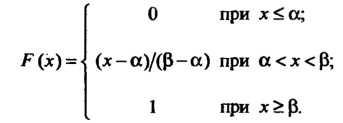
Для этой случайной величины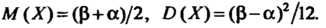
Показательное распределение определяется формулой

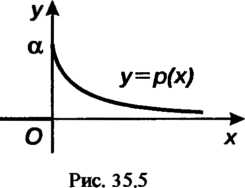
Кривая распределения вероятноястей этой величины представлена на рис. 35.5. Функция распределения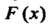 В этом случае имеет вид
В этом случае имеет вид
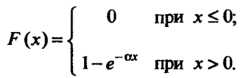
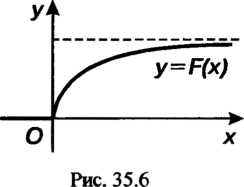
График функции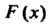 Изображен на рис. 35.6. Для этой случайной величины
Изображен на рис. 35.6. Для этой случайной величины 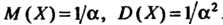
Нормальным распределением (или распределением Гаусса) называется распределение случайной величины, определяемое формулой
Параметры распределения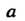 И
И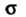 нормальной случайной величины
нормальной случайной величины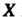 Имеют следующие значения:
Имеют следующие значения: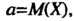
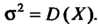 График функции
График функции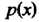 Называют нормальной кривой или кривой Гаусса. На рис. 35.7 представлены три кривые при одном
Называют нормальной кривой или кривой Гаусса. На рис. 35.7 представлены три кривые при одном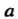 И различных
И различных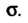
Вероятность попадания значений нормально распределенной случайной величины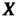 В интервал
В интервал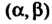 Определя
Определя
Ется формулой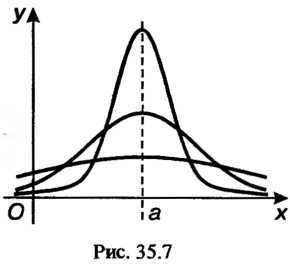
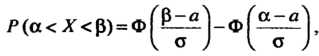 (35.21)
(35.21)
Где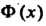 - функция Лапласа:
- функция Лапласа:
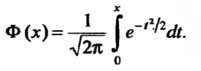 (35.22)
(35.22)
С помощью этой функции выражается вероятность неравенства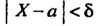 Для
Для
Нормальной случайной величины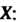
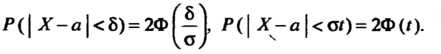
При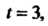 Т. е.
Т. е.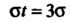 Последнее равенство принимает вид
Последнее равенство принимает вид
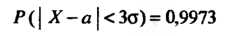
И выражает правило трех сигм: если случайная величина распределена по нормальному закону, то модуль ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
Пример 35.7. Найти вероятность попадания в интервал (4,9) значений нормальной случайной величины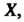 Для которой математическое ожидание
Для которой математическое ожидание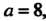 Среднее квадратическое отклонение
Среднее квадратическое отклонение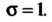
Применяем формулу (35.21), которая в данном случае примет ввд
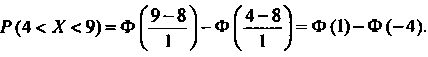
Поскольку функция Лапласа (35.22) является нечетной, то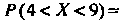
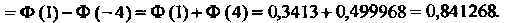 (Значения
(Значения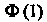 И
И
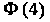 Найдены по таблице значений функции Лапласа.)
Найдены по таблице значений функции Лапласа.)
| < Предыдущая | Следующая > |
|---|