35.7. Основные теоремы теории вероятностей

Теорема 35.1 (теорема Чебышева). Если случайные величины 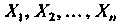Попарно независимы, имею математические ожидания и дисперсии, каждая из которых ограничена одним и тем же числом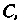То для любого числа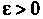Выполняется неравенство

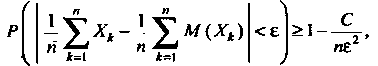
Откуда

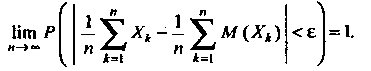(35.23)

В частном случае, когда все случайные величины имеют одно и то же математическое ожидание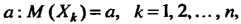Равенство (35.23) принимает ввд

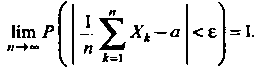
Теорема 35.2 (теоремаБернулли). Если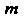- число наступлений события 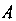в п независимых испытаниях и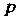- вероятность наступления события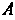В каждом из испытаний, то при любом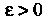

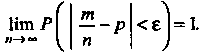
Теорема 35.3 (теорема Ляпунова). Если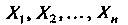— независимые слу

Чайные величины, имеющие одно и то же распределение с математическим ожиданием а и дисперсией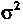, то при неограниченном возрастании п закон распределения

Суммы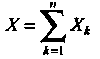Неограниченно приближается к нормальному.

Теорема 35.4 (локальная теорема Лапласа). Если вероятность наступления события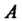В каждом из п независимых испытаний равна одной и той же постоянной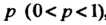, то вероятность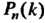Того, что во всех этих испытаниях событие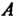Наступит ровно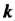Раз, приближенно выражается формулой

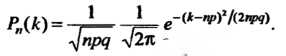(35.24)

Вероятность (35.24) можно вычислить так:

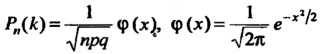
При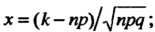Для функции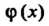Составлены таблицы.

Теорема 35.5 (интегральная теорема Лапласа). Если вероятность наступления события А в каждом из п независимых испытаний равна одной и той же постоянной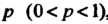, то вероятность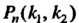Того, что в этих испыта

Ниях событие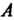Наступит не менее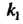Раз и не более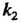Раз, приближенно выражается формулой

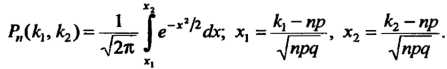(35.25)

Вероятность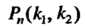Можно подсчитать по формуле

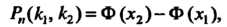(35.26)

Где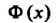- функция Лапласа (см. формулу (35.22)).

Пример 35.8. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена не менее 70 и не более 80 раз.

По условию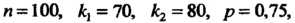Поэтому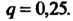Воспользу

Емся формулой (35.26), предварительно вычислив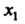И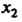По второй и третьей формуле (35.25):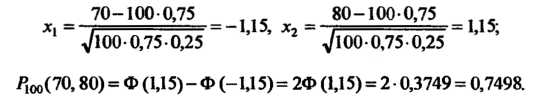

Гпава 36

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ И МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

< Предыдущая		Следующая >