35.5. Некоторые другие числовые характеристики

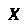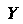Ковариацией двух случайных величинИНазывается математическое ожидание произведения их отклонений от соответствующих математических ожиданий:

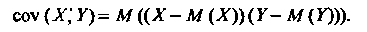
Для ковариации верны равенства:

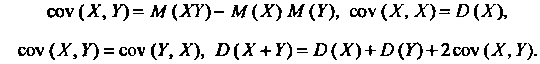
Если случайные величины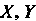Независимы, то их ковариация равна нулю:

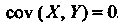. Если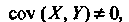То случайные, величины зависимы.

Коэффициентом корреляции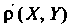Случайных величины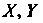Называется

Отношение их ковариации к произведению средних квадратических отклонений этих величин:

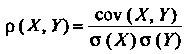
Свойства коэффициента корреляции: 1)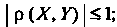2) если величины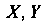

Независимы, то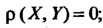3) если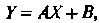То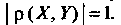

Начальным моментом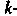Го порядка случайной величины X называется математическое ожидание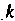-й степени этой величины: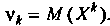Центральным моментом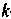-го порядка случайной величины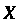Называется математическое ожидание 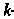¦й степени отклонения этой величины от ее математического ожидания 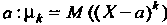I. Математическое ожидание и дисперсия случайной величины - частные случаи моментов, а именно: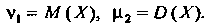

< Предыдущая		Следующая >