35.4. Дисперсия случайной величины

Дисперсией (или рассеянием) случайной величины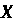Называется математическое ожидание квадрата ее отклонения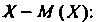

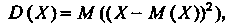(35.13)

Дисперсия случайной величины обладает следующими свойствами.

1. Дисперсия постоянной величины (равна нулю: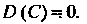

2.  Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: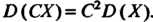

3.  Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: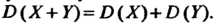

4.  Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: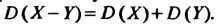

Дисперсия дискретной случайной величины с законом распределения (35.1) определяется формулой

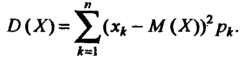(35.15)

Если дискретная случайная величина имеет закон распределения (35.2), то

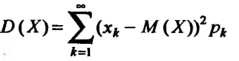(35.16)

При условии, что этот ряд сходится.

Дисперсия непрерывной случайной величины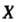С плотностью распределения 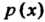Определяется формулой

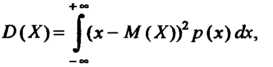
(35.17)

Если этот интеграл сходится, или

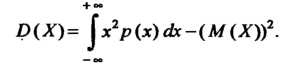
Средним квадратическим отклонением (или стандартным отклонением)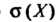 случайной величины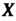Называется корень квадратный из ее дисперсии:

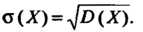(35.18)

Пример 35.5. Найтидисперсиюслучайнойвеличины, указаннойвпримере35.1. В примере 35.4. было “показано, что для данной случайной величины 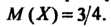По формуле (35.17) находим

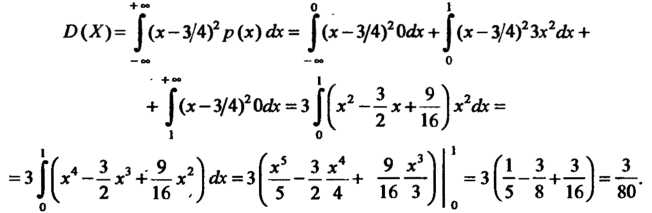
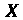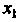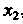Пример 35.6. Дискретная случайная величинаМожет принимать только два значенияИ, причем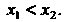Известны вероятность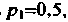

Математическое ожидание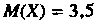И дисперсия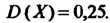Найти закон

Распределения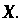

Поскольку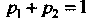(см. вторую формулу (35.1)) и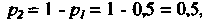То

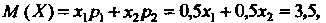Откуда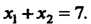По формуле (35.15)

Находим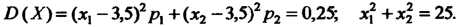Решая систему

Уравнений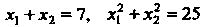И учитывая условие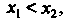Получаем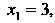

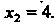Следовательно,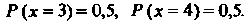

< Предыдущая		Следующая >