35.3. Математическое ожидание случайной величины

Математическое ожидание случайной величины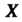С законом распределения (35.1) определяется формулой

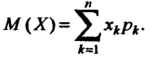(35.9)

Если случайная величина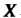Задана законом распределения (35.2), то

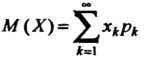(35.10)

При условии, что ряд сходится.

Математическое ожидание называется средним значением, а также центром распределения. Для математического ожидания употребляются и другие обозначения: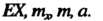

Математическое ожидание непрерывной случайной величины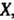, все значения которой принадлежат отрезку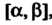, определяется формулой

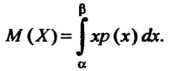(35.11)

Если случайная величина может принимать любые значения из промежутка 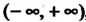, то

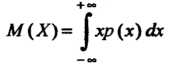(35.12)

При условии, что интеграл сходится.

Математическое ОНЬЩшие случайной величины обладает следующими свойствами.

1.  Математическое ожидание случайной величины заключено между ее наименьшим и наибольшим значениями.

2.  Математическое ожидание постоянной равно этой постоянной: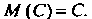

3.  Постоянный множитель можно выносить за знак математического ожидания, т. е.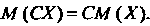

4.  Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий: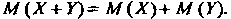

5.  Математическое ожидание произведения двух независимых величин равно произведению их математических ожиданий: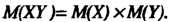

Пример 3S.3. Найти математическое ожидание дискретной случайной величины по ее закону распределения, заданному схемой

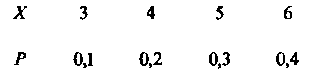
По формуле (35.9) находим: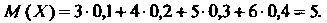

Пример 35.4. Найти математическое ожидание непрерывной случайной величины, указанной в примере 35.1.

По формуле (35.12) получаем

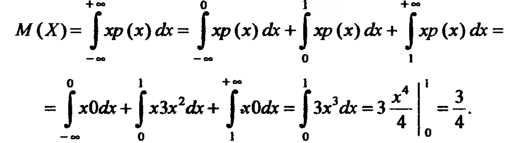
Название «математическое ожидание» происходит от понятия «ожидаемое значение выигрыша» (математическое ожидание выигрыша), впервые появившегося в теории азартных игр в трудах Б. Паскаля и X. Гюйгенса в XVII в. Термин «математическое ожидание» ввел П. Лаплас (1795). В полной мере это понятие впервые оценено и использовано П. Л. Чебышевым.

< Предыдущая		Следующая >