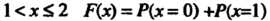35.2. Функция распределения. Плотность распределения
Функцией распределения случайной величины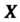 Называется функция
Называется функция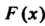 действительной переменной, определяемая равенством
действительной переменной, определяемая равенством
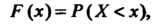
Где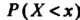 I — вероятность того, что случайная величина
I — вероятность того, что случайная величина Примет значение,
Примет значение,
Меньшее х. Вероятность того, что случайная величина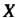 Примет значение из полуинтервала
Примет значение из полуинтервала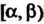 , равна разности значений ее функции распределения в концах этого промежутка
, равна разности значений ее функции распределения в концах этого промежутка
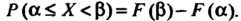
Свойства функции распределения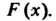
1. Все значения функции распределения принадлежат отрезку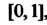 , т. е.
, т. е.
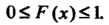
2. Функция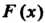 Является неубывающей:
Является неубывающей: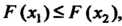 Если
Если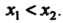
3.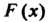 Непрерывна слева при любом
Непрерывна слева при любом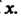
4.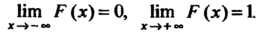
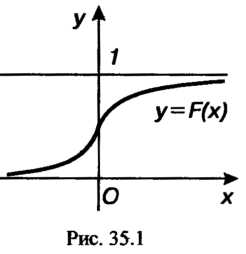
График функции распределения целиком расположен в полосе между прямыми 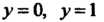 (рис. 35.1).
(рис. 35.1).
Функция распределения дискретной случайной величины имеет вид
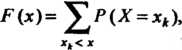
(35.4)
Где символы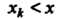 Означают, что суммируются вероятности тех значений, которые
Означают, что суммируются вероятности тех значений, которые
Меньше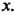 Функция
Функция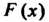 Для дискретной случайной величины является разрывной.
Для дискретной случайной величины является разрывной.
Случайная величина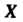 Называется непрерывной, если существует неотрицательная функция
Называется непрерывной, если существует неотрицательная функция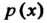 Такая, что
Такая, что
X
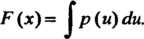
(35.5)
Функция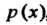 , входящая в это равенство, называется плотностью распределения вероятностей случайной величины
, входящая в это равенство, называется плотностью распределения вероятностей случайной величины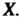 График функции
График функции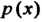 Называется кривой распреде
Называется кривой распреде
Ления. Вероятность попадания значений случайной величины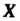 В полуинтервал
В полуинтервал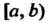 равна определенному интегралу от плотности распределения
равна определенному интегралу от плотности распределения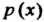 По отрезку
По отрезку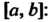
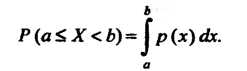
Свойства функции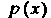 — плотности распределения.
— плотности распределения.
1. Функция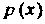 Является неотрицательной:
Является неотрицательной: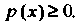
2. В точках дифференцируемое™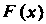 Производная функции распределения равна плотности распределения вероятностей:
Производная функции распределения равна плотности распределения вероятностей:
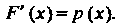 (35.7)
(35.7)
3. Интеграл по бесконечному промежутку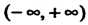 От плотности распределения вероятностей
От плотности распределения вероятностей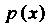 Равен единице:
Равен единице:
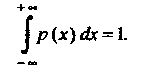
(35.8)
Пример 35.1. Случайная величина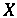 Задана функцией распределения
Задана функцией распределения 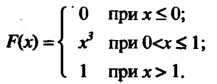 Найти плотность распределения
Найти плотность распределения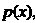 , построить трафики функций
, построить трафики функций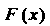 И
И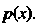
В соответствии с равенством (35.7) находим
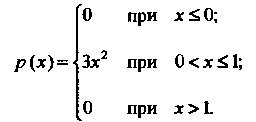
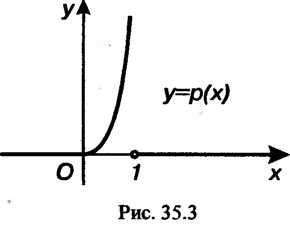
Графики функций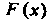 И
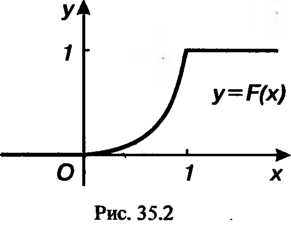
И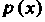 Изображены на рис. 35.2 и 35.3.
Изображены на рис. 35.2 и 35.3.
Пример 35.2. Найти функцию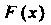 Для дискретной случайной величины, закон распределения которой задан схемой
Для дискретной случайной величины, закон распределения которой задан схемой
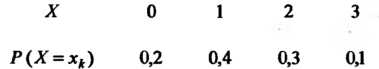
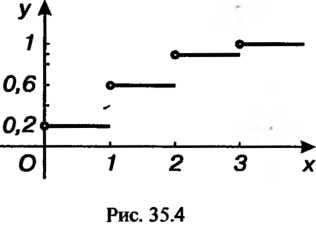
Функцию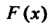 Строим с помощью формулы (35.4). При
Строим с помощью формулы (35.4). При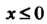
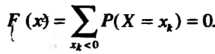 Если
Если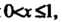
То,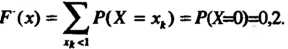
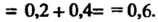 Если
Если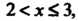 То
То
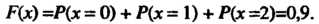
При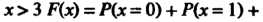
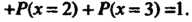 График функции
График функции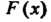 Изображен на рис. 35.4.
Изображен на рис. 35.4.
| < Предыдущая | Следующая > |
|---|