34.5. Формула полной вероятности. Формулы Бейеса

Предположим, что событие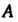Может осуществляться с одним из несовместных событий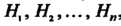, для которых известны вероятности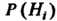И условные вероятности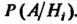. Другими словами, положим, что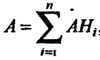, тогда

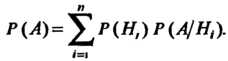(34.10)

Это равенство называют формулой полной вероятности.

Произведен опыт, в результате которого появилось событие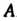. Требуется найти условные вероятности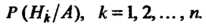

Согласно теореме умножения вероятностей

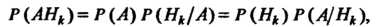
Откуда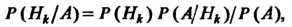

Или

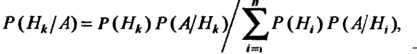(34.,,)

Где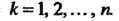

Формулы (34.ii) носят название формул Бейеса.

В применениях формул Бейеса события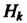Называют гипотезами,

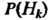- априорными вероятностями гипотез,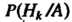- апостериорными вероят

Ностями этих гипотез.

Пример 34.7. Имеется 5 урн с белыми и черными шарами: 2 урны - по 2 белых и 3 черных шара (состав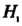), 2 урны - по i белому и 4 черных шара (состав),

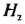1 урна - 4 белых и 1 черный шар (состав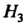). Из одной наудачу выбранной урны вынут шар, который оказался черным (событие А). Чему равна апостериорная вероятность того, что шар вынут из урны второго состава?

Полагая в (З4.и)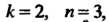Получаем формулу, которой надлежит пользо

Ваться в данном случае:

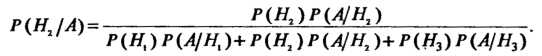
Найдем соответствующее вероятности: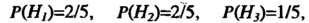

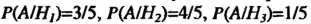И подставим их в данную формулу

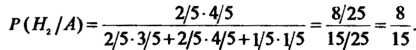
Аналогично можно найти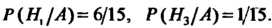

Гпава 35

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ, ИХ РАСПРЕДЕЛЕНИЯ И ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ

< Предыдущая		Следующая >