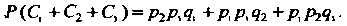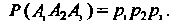34.4. Условная вероятность. Теорема умножения вероятностей. Независимость событий

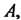Вероятность событияПри условии, что произошло событиеНазывается условной вероятностью события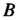И обозначается так: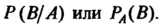

Условные вероятности определяются формулами

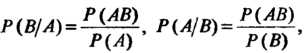
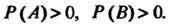
Теорема 34.1. Вероятность произведения двух событий равна произведению вероятностей одного из них на условную вероятность другого при условии, что первое событие произошло:

По определению, событие В не зависит от события А, если

В этом случае также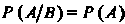, т. е. событие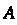Не зависит от события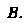

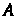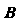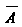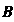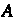Свойство независимости событий является взаимным. Если событияИНезависимы, то независимы событияИ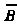,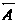И,И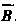Если события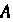И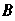 независимы, то формулы (34.4) с учетом равенства (34.5) принимают вид

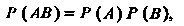
Т. е. вероятность произведения независимых событий равна произведению их вероятностей.

Теорема 34.2. Вероятность произведения п событий равна произведению вероятностей одного из них на условные вероятности всех остальных в предположении, что все предыдущие события наступили:

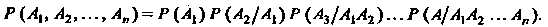(34.6)

В частности, для трех событий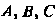Эта формула имеет вид

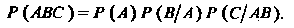(34.7)

События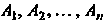Называются независимыми в совокупности (или просто

Независимыми), если каждое из них и произведение любого числа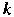Остальных 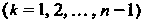Являются независимыми.

Замечание. Из попарной независимости событий не следует их независимость в совокупности.

Если события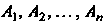Независимы, то

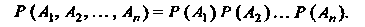(34.8)

Если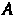- появление хотя бы одного из независимых событий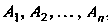, то

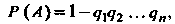(34.9)

Где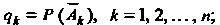(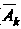- событие, противоположное).

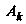Если все независимые события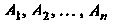Имеют одну и ту же вероятность

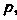, то вероятность появления хотя бы одного из них определяется формулой

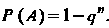
Пример 34.4. В урне имеется 6 красных, 8 синих и 4 белых шара. Каждое испытание состоит в том, что из урны берут наудачу один шар и не возвращают обратно. Найти вероятность того, что при первом испытании будет вынут красный шар (событие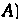I, при втором - синий (событие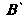), при третьем - белый (событие).

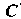ПосколькуТо по

Формуле (34.7) получаем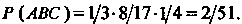

Пример 34.5. В каждом из трех ящиков имеется по 24 детали; при этом в первом ящике 18, во втором 20, в третьем 22 стандартные детали. Из каждого ящика берут по одной детали. Найти вероятность того, что все три извлеченные детали окажутся стандартными.

Введем обозначения: извлечение стандартной детали из первого ящика-событие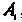, из второго - событие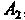, из третьего - событие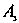, тогда

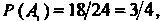
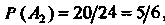
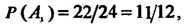По формуле

(34.8) при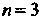Получаем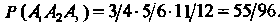

Пример 34.6. Три стрелка в одинаковы и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 0,9, вторым - 0,8, третьим - 0,7. Найти вероятность того, что: а) только один из стрелков попадет в цель; б) только два стрелка попадут в цель; в) все три стрелка попадут в цель.

Введем обозначения: поражение'цели первым стрелком -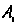, вторым.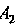, третьим -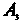; попадание в цель только первым стрелком -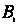, только вторым стрелком —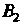, только третьим —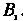Пусть

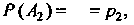
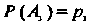, тогда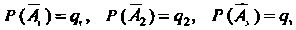. Поскольку,

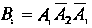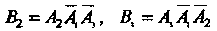И события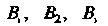Несовместны, то вероятность

Того, что только один стрелок попадет в цель, выражается формулой

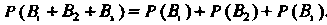, Так как,

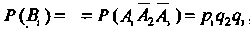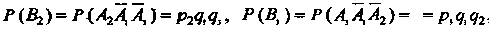, то

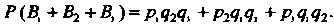
Пусть- попадание в цель только вторым и третьим стрелками,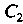- только первым и третьим,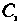- только первым и вторым, т. е.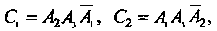

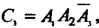Тогда вероятность того, что только два стрелка попадут в цель, выразится формулой

(II)

Вероятность того, что три стрелка попадут в цель, определяется формулой

(III)

По условию задачи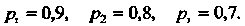Следовательно,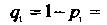

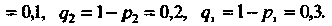Подставляя эти значения в формулы (I) -

(Ш), находим искомые вероятности: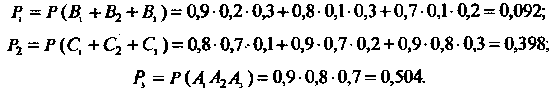

< Предыдущая		Следующая >