34.3. Различные определения вероятности события

Классическое определение вероятности. Вероятность события А определяется формулой

(34.1)

Где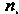I - число всех равновозможных, образующих полную группу элементарных исходов опыта,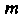- число элементарных исходов, благоприятствующих событию А. Свойства вероятности события: 1) вероятность достоверного события равна единице; 2) вероятность невозможного события равна нулю; 3) вероятность случайного события выражается положительным числом, меньшим единицы; 4) вероятность любого события удовлетворяет неравенствам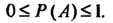

Геометрическое определение вероятности. Если событие А—попадание в область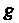Точки, брошенной в область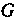, то его вероятность определяется формулой

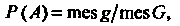(34.2)

Где mesg — мера области g (длина, площадь, объем). Для одномерной двумерной и трехмерной области эта формула соответственно принимает вид

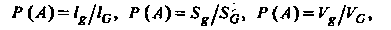
Где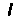— длина,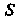— площадь,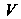— объем соответствующей области.

Статическое определение вероятности. Относительная частота события А (или просто частота) определяется формулой

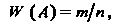(34.3)

Где т — число опытов, в которых появилось событие А,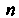— число всех проведенных опытов. Условной называется частота одного события, вычисленная при условии, что другое событие наступило. Частота события обладает теми же простейшими свойствами, что и вероятность, а также следующими свойствами: а) частота суммы двух несовместимых событий равна сумме частот этих событий: 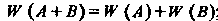; б) частота произведения двух событий равна произведению частоты одного на условную частоту другого: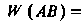

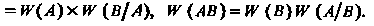
Вероятностью события называется число, около которого группируются значения относительной частоты данного события в различных сериях большого числа испытаний.

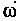Аксиоматическое определение вероятности. Пространством элементарных событий называют произвольное множество, а его элементы элементарными событиями. Эти понятия являются первоначальными. В реальных опытах элементарным событиям соответствуют взаимоисключающие итоги опыта. Подмножества множества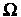Называют событиями и обозначают заглавными буквами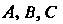И т. п. Пустое множество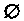Называют невозможным событием, а множество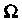- достоверным событием. Случайным событием называют любое собственное (т. е. отличное отИ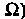I подмножество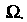Событие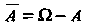

Называют противоположным событию А; событие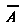Означает, что А не произошло. События Л и В называют несовместными, если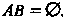

Пусть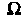— пространство элементарных событий,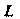— некоторая система случайных событий. Система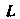Случайных событий называется алгеброй событий, если выполнены условия: 1)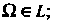2) если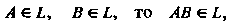

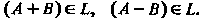Из этих условий следует, что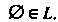Алгебра событий

Называется о-апгеброй или борелевской алгеброй, если из того, что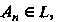

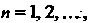Следует

Числовая функция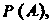Определенная на алгебре событий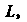Называется ве

Роятностью, если выполнены следующие аксиомы.

1.  Каждому событию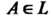Ставится в соответствие неотрицательное число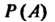- его вероятность, т. е.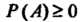Для любого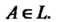

2.  Вероятность достоверного события равна единице: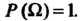

3.  Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т. е.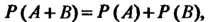Если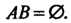

4.  Для любой убывающей последовательности

Событий из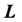Такой, что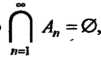Справедливо равенство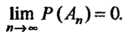

Тройка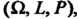В которой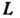Является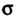-алгеброй и функция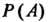Удовле-

>ряет аксиомам 1 - 4, называется вероятностным пространством.

Простейшие следствия из аксиом вероятности.

1.  Сумма вероятностей противоположных событий равна единице:

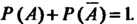Если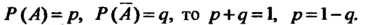

2.  Вероятность невозможного события равна нулю: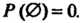

3.  Для любых событий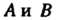Верны соотношения

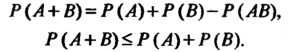
4.  Если события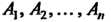Попарно несовместны (т. е.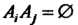При любых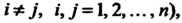То

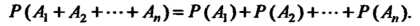
5.  Для любых событий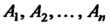Выполняется неравенство

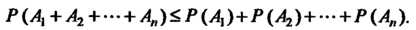
6.  Если событие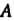Влечет событие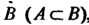, то

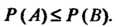
7.  Вероятность любого события выражается неотрицательным числом, не превосходящим единицы: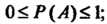Другими словами, область значений функции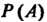Принадлежит отрезку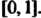

8.  Если события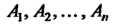— попарно несовместны и 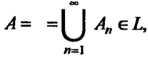то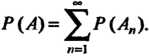

9.  Если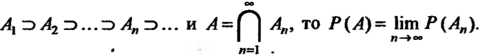

10.  Если.

Пример 34.1. Найти вероятность появления верхней грани с числом очков, кратным 3, при-бросании игрального кубика.

Поскольку всего элементарных исходов шесть, а благоприятных исходов лва:

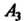(появилось 3 очка),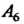(появилось 6 очков), то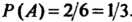

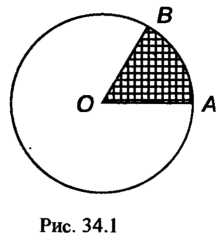
Пример 34.2. Производится стрельба по мишени, имеющей форму круга и равномерно вращающейся вокруг центра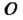(рис. 34.1). Попадание в круг - событие достоверное. Сектор, площадь которого равна одной шестой части площади всего круга, окрашена в черный цвет. Найти вероятность попадания в сектор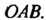

В данном случае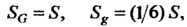Где

- площадь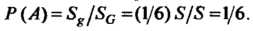Рассматриваемого круга, поэтому

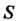
Пример 34.3. В результате 20 выстрелов по мишени получено 15 попаданий. Какова относительная частота попаданий?

Так как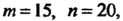То по формуле (34.3) получаем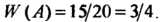

< Предыдущая		Следующая >