33.2. Метод Эйлера

Пусть требуется решить задачу Коши: найти решение дифференциального уравнения

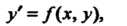(33.1)

Удовлетворяющее начальному условию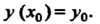

При численном решении уравнения (33.1) задача ставится так: в точках 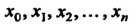Найти приближения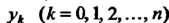Для значений точного

Решения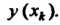Разность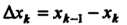Называется шагом сетки. Во многих

Случаях величину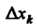Принимают постоянной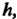Тогда

Метод Эйлера основан на непосредственной замене производной разностным отношением по приближенной формул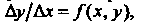еГде

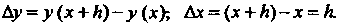
Приближенное значение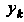В точке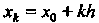Вычисляется по формуле

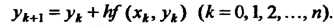(33.3)

Пример 33.4. Методом Эйлера найти значения решения дифференциального уравнения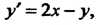Для которого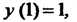В пяти точках отрезка 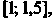Приняв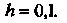

По формулам (33.2) находим точки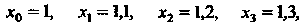

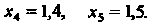Значения искомой функции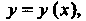Удовлетворяющей

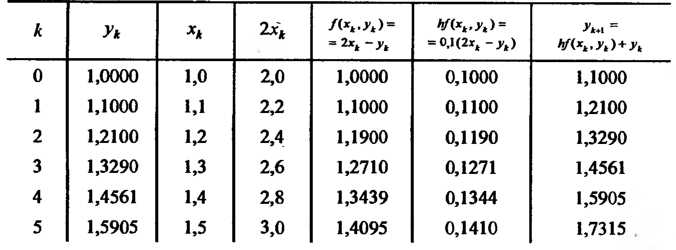
Условию данной задачи Коши, вычисляем по формуле (33.3). Результаты вычислений занесены в табл. 33.1.

Таблица 33.1

< Предыдущая		Следующая >