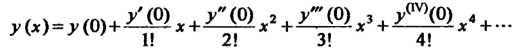33.1. Интегрирование дифференциальных уравнений с помощью рядов

Решения многих дифференциальных уравнений не выражаются в элементарных функциях. В этих случаях пользуются приближенными методами интегрирования дифференциальных уравнений. Одним из таких методов является представление решения уравнения в виде степенного ряда; сумма конечного числа членов этого ряда будет приближенно равна искомому решению. Указанный степенной ряд находят способом неопределенных коэффициентов или способом, основанным на применении ряда Тейлора (Маклорена).

Способ неопределенных коэффициентов особенно удобен в применении к линейным уравнениям, т. е. уравнениям вида

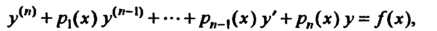
И состоит в следующем. Если все коэффициенты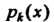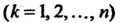Этого

Уравнения и свободный член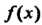Разлагаются в ряды по степеням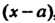, схо

Дящиеся в интервале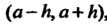, то искомое решение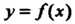Также представ

Ляется степенным рядом

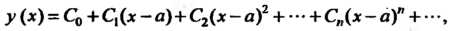
Сходящимся в этом же интервале. Подставляя в уравнение функцию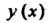И ее

Производные, приравнивают коэффициенты при одинаковых степенях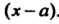Из

Полученных при этом уравнений и заданных начальных условий находят коэффициенты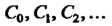

Способ основанный на применение ряда Тейлора (Маклорена), заключается в последовательном дифференцировании данного уравнения. Это дает возможность найти значения производных, входящих в выражения для коэффициентов ряда

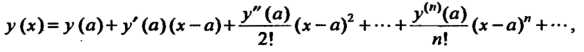
Являющегося решением уравнения.

Пример 33.1. Найти первые пять членов разложения в ряд решения уравнения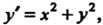Удовлетворяющего условию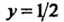При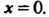

©

Найдем выражения для трех последующих производных, дифференцируя данное. уравнение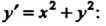

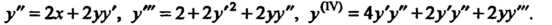
Вычислим значения этих производных при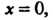Принимая во внимание началь

Ное условие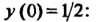

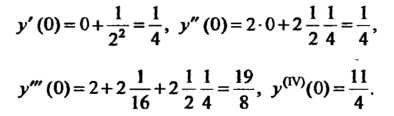
Подставляя эти значения в формулу (I), получаем

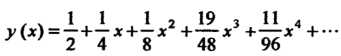
Пример 33.2. С помощью степенного ряда проинтегрировать уравнение 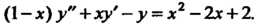 Пусть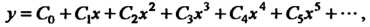Тогда

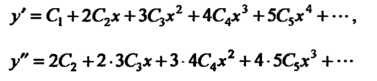
Подставляя выражения для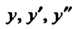В данное уравнение, получаем

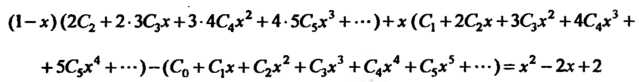
Или  ^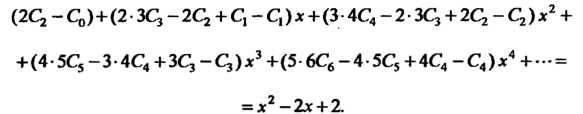

Так как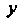— решение уравнения, то последнее равенство выполняется тождественно; коэффициенты при одинаковых степенях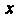В обеих частях равенства равны между собой:

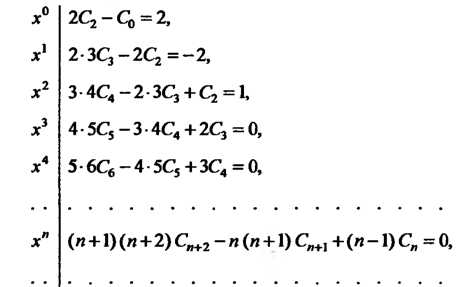
Решая эту систему, находим

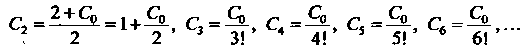
Таким образом, все коэффициенты, начиная с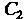, выражены через коэффициент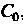, который остается произвольным; остается произвольным и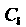(этот коэффициент не входит в полученную систему). Следовательно, искомое решение представляется рядом

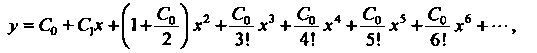
Сходящимся при всех х. Это решение является общим:

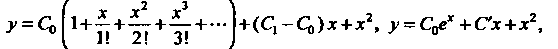
Где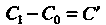- произвольная постоянная.

Пример 33.3. Найти первые пять членов разложения в ряд частного решения уравнения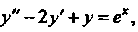Удовлетворяющего начальным условиям: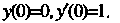

Пусть искомое решение представляется сходящимся степенным рядом

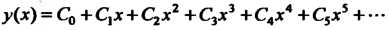Дважды дифференцируя этот ряд

В его интервале сходимости, получаем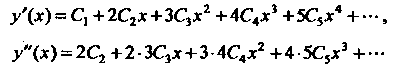

При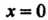Имеем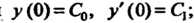Принимая во внимание начальные усло

Вия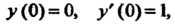Находим два первых коэффициента разложения для

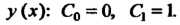Подставив в данное дифференциальное уравнение выражения для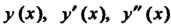И разложение в ряд функции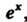, получим

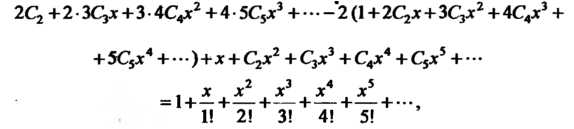
Или

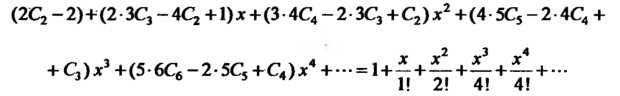
Приравнивая коэффициенты при одинаковых степенях х в обеих частях этого равенства, получаем систему уравнений для определения коэффициентов

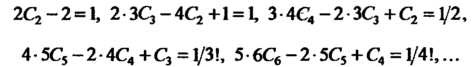
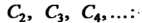
Решая эту систему, находим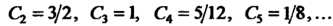Таким обра

Зом, частное решение выражается формулой

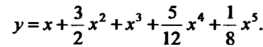
< Предыдущая		Следующая >