33.3. Метод Рунге - Кутта
Пусть требуется найти численное решение уравнения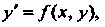
Удовлетво
Ряющее условию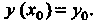
Идея метода Рунге - Кутта состоит в представлении разности
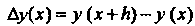(33.4)
В виде суммы поправок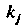
С коэффициентами
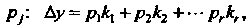Где
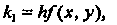
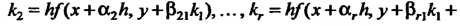
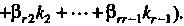
Коэффициенты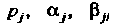
Находят сравнением разложени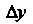й
И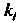
По степеням
В случае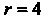
Получаем
(33.5)
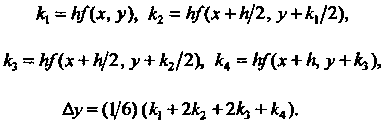(33.6)
При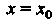
С помощью формул (33.4) - (33.6) находим
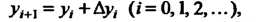(33.7)
Где
(33.8)
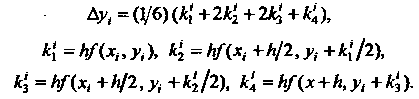(33.9)
Метод Рунге - Кутта - один из наиболее употребительных методов повышенной точности.
Пример 33.5. Методом Рунге - Кутта найти решение задачи Коши для уравнения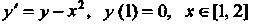
В первых пяти точках, взяв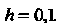
Поскольку в данном случае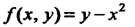
И в силу условия
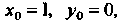То
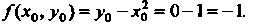По формулам (33.9) находим: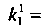
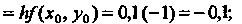
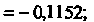
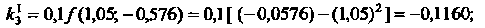
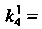
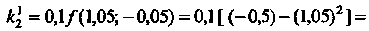
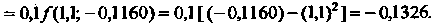По формуле (33.8) вычислим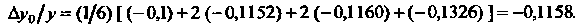
Значение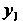
Вычислим по формуле
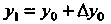(см. формулу (33.7) при
):
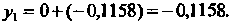Таким образом, получено приближенное значение
Решения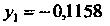
При
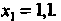
С помощью формул (33.9) при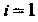
Найдем приближенное значение
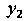При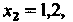 
Решив новую задачу Коши для того же уравнения
»
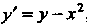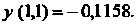
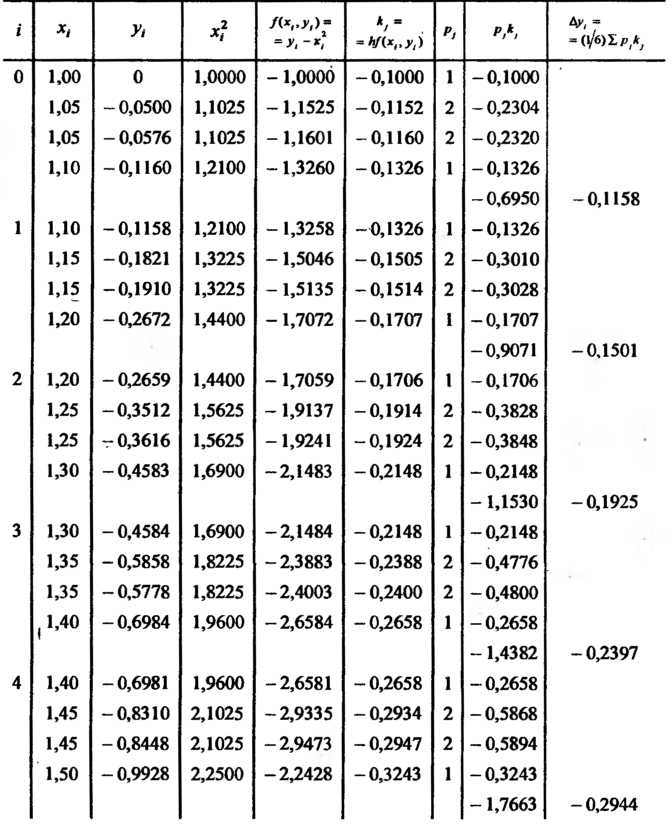
Аналогично находим значения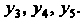
Результаты решения исходной зада
Чи представлены в табл. 33.2, из которой следует, что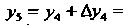
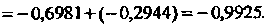
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
СЛУЧАЙНЫЕ СОБЫТИЯ И ИХ ВЕРОЯТНОСТИ
| < Предыдущая | Следующая > |
|---|
