32.2. Формула трапеций

Формула трапеций имеет вид

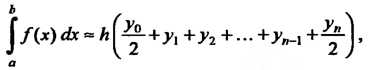(32.5)

Где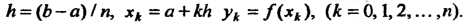

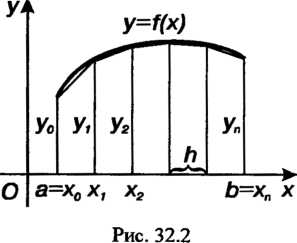
Правая часть этой формулы выражает площадь фигуры, состоящей из трапеций, высота каждой из которых равна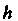(рис. 32.2). Если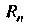- остаточный член приближенной формулы (32.5), то

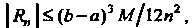(32.6)

Где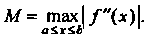

Трапеций, приняв

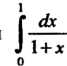
В данном случае по расчетной формуле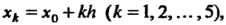

Где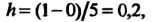Получаем

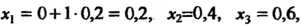
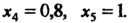Так как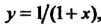 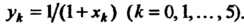 Находим значение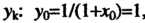

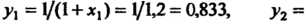
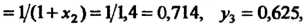
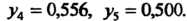
По формуле (32.5) получаем

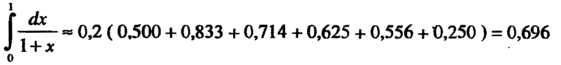
Пример 32.4. На сколько частей нужно разбить промежуток интегрирования, чтобы по формуле трапеций вычислить интеграл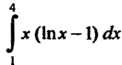С точностью?

Для определения числа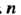Отрезков, на которые нужно разбить промежуток интегрирования, воспользуемся формулой (32.6). Неравенство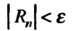Будет выполнено, если ~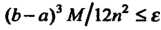, откуда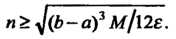Поскольку

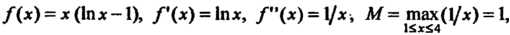То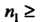

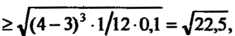
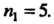Аналогично находим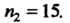

< Предыдущая		Следующая >