32.1. Формулы прямоугольников
Формулы прямоугольников имеют вид
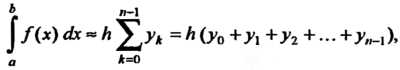 (32.1)
(32.1)
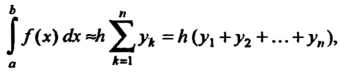 (32.2)
(32.2)
Где
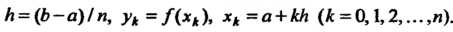 (32.3)
(32.3)
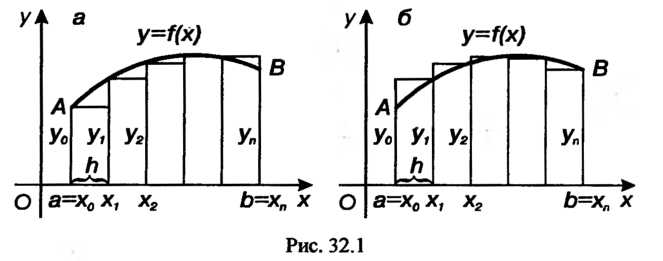
Формула (32.1) называется формулой левых прямоугольников (рис. 32.1, а), формула (32.2) - формулой правых прямоугольников (рис. 32.1, б).
Абсолютная погрешность метода прямоугольников определяется неравенством
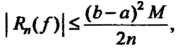 (32.4)
(32.4)
Где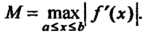
Пример 32.1. По формулам прямоугольников, приняв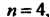 вычислить
вычислить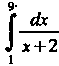
В данном случае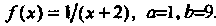 . С помощью формул (32.3) находим
. С помощью формул (32.3) находим
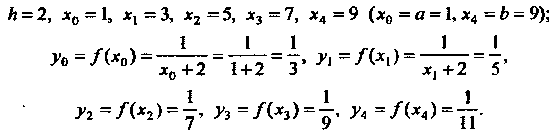
По формулам (32.1) и (32.2) получаем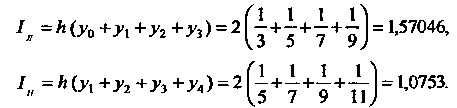
Пример 32.2. На сколько частей следует разбить промежуток интегрирования, чтобы с точностью до 0,1 вычислить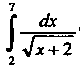 ?
?
Абсолютная погрешность при вычислении определенного интеграла по методу прямоугольников определяется формулой (32.4). Если ставится задача, чтобы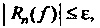 Т. е.
Т. е.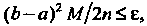 То
То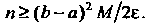 В данном случае
В данном случае
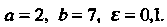 Так как
Так как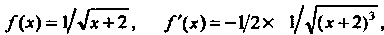
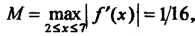 То
То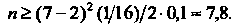 Поскольку и - целое чис
Поскольку и - целое чис
Ло, можно принять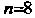 (для удобства вычислений можно взять
(для удобства вычислений можно взять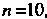 Так как
Так как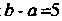 ).
).
| < Предыдущая | Следующая > |
|---|