31.3. Интерполяционный многочлен Ньютона
Интерполяционным многочленом Ньютона называется многочлен
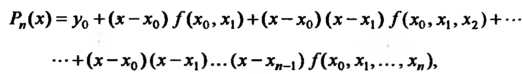 (31.13)
(31.13)
В котором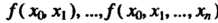 I - разделенные разности различных порядков.
I - разделенные разности различных порядков.
Этот многочлен удовлетворяет условиям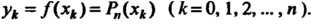
Интерполяционной формулой Ньютона называется формула
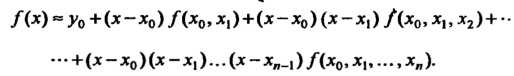 (31.14)
(31.14)
Замечание 1. Поскольку любой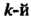 Член многочлена Ньютона зависит только от
Член многочлена Ньютона зависит только от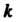 Первых узлов интерполяции и от значений функции в этих узлах, добавление новых узлов вызывает в формуле (31.13) лишь добавление новых членов без изменения первоначальных. Это является существенным преимуществом многочлена Ньютона по сравнению с многочленом Лагранжа.
Первых узлов интерполяции и от значений функции в этих узлах, добавление новых узлов вызывает в формуле (31.13) лишь добавление новых членов без изменения первоначальных. Это является существенным преимуществом многочлена Ньютона по сравнению с многочленом Лагранжа.
Замечание 2. В силу единственности интерполяционного многочлена 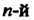 Степени интерполяционный многочлен Ньютона перегруппировкой членов можно преобразовать в интерполяционный многочлен Лагранжа и обратно.
Степени интерполяционный многочлен Ньютона перегруппировкой членов можно преобразовать в интерполяционный многочлен Лагранжа и обратно.
В случае равноотстоящих узлов интерполяции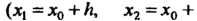
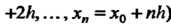 | из формулы (31.14) с учетом (31.12) получается интерполяционная формула Ньютона для «интерполирования вперед»:
| из формулы (31.14) с учетом (31.12) получается интерполяционная формула Ньютона для «интерполирования вперед»:
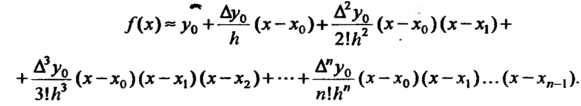 (31.15)
(31.15)
Формула (31.15) удобна при интерполировании функций для значений х, близких к наименьшему узлу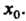
Интерполяционная формула Ньютона для «интерполирования назад»:
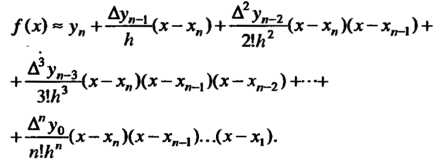 (31.16)
(31.16)
Формула (31.16) удобна при интерполировании функций для значений х, близких к наибольшему узлу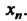
Замечание 3. В формуле (31.15) в коэффициенты многочлена входят конечные разности различных порядков, принадлежащие верхней (нисходящей) строке таблицы разностей (см. табл. 31.1). В формуле (31.16) в коэффициенты многочлена входят разности различных порядков, принадлежащие нижней (восходящей) строке таблицы разностей.
Пример 31.4. Найти интерполяционный многочлен Ньютона для функции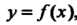 , если известны ее значения:
, если известны ее значения: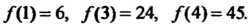
В данном случае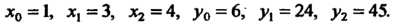 Отметим, что
Отметим, что
Узлы не являются равноотстоящими (так как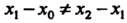 ). Интерполяционный
). Интерполяционный
Многочлен (31.13) при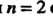 С учетом равенств (31.11) принимает вид
С учетом равенств (31.11) принимает вид
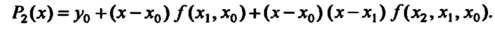
Вычисляем разделенные разности 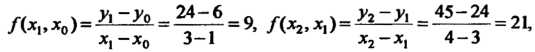
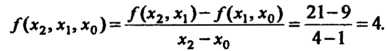
Подставляя в выражение для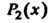 Соответствующие значения, находим интерпо
Соответствующие значения, находим интерпо
Ляционный многочлен Ньютона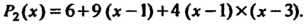
Замечание 4. Раскрывая скобки и группируя члены, получаем
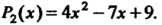
Пример 31.5. Найти интерполяционный многочлен Ньютона для функции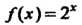 По ее значениям в точках
По ее значениям в точках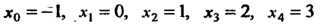 И вычислить
И вычислить И
И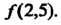
Вычислим сначала значения функции в данных равноотстоящих узлах:
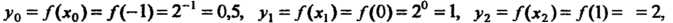
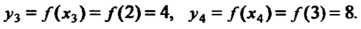 Составим таблицу разностей различных порядков (табл. 31.3).
Составим таблицу разностей различных порядков (табл. 31.3).
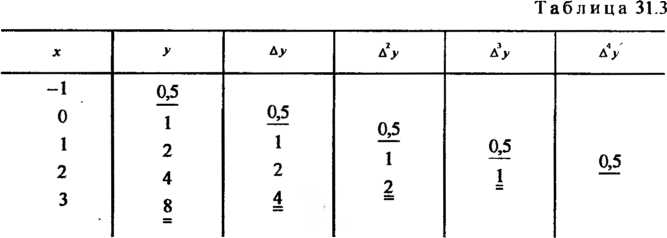
Числа, подчеркнутые одной чертой входят в интерполяционную формулу Ньютона для «интерполирования вперед». Многочлен в правой части формулы (31.15) в данном случае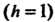 Принимает вид
Принимает вид
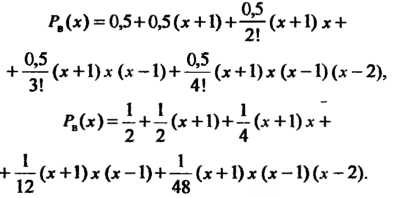
С помощью этого многочлена вычислим значение функции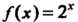 При
При
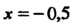 (значение аргумента ближе к
(значение аргумента ближе к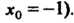 Подставляя значение
Подставляя значение
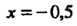 В формулу (I), находим
В формулу (I), находим
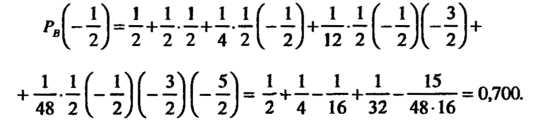
Числа табл. 31.3, подчеркнутые двумя чертами (и число 0,5 в столбце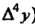 I, входят в интерполяционную формулу Ньютона для «интерполирования назад». Многочлен в правой части формулы (31.16) в данном случае принимает ввд
I, входят в интерполяционную формулу Ньютона для «интерполирования назад». Многочлен в правой части формулы (31.16) в данном случае принимает ввд
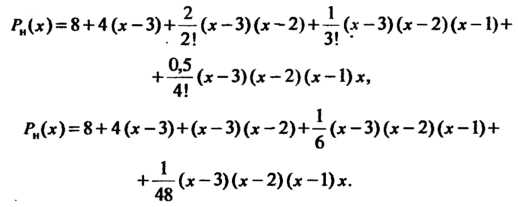
С помощью многочлена (II) вычислим значение данной функции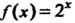 При
При
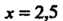 (это значение аргумента ближе к
(это значение аргумента ближе к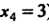 ). Подставляя значение
). Подставляя значение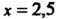 В
В
Формулу (II), получаем
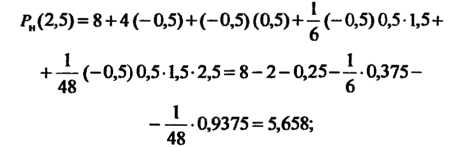
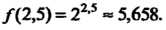 Следовательно,
Следовательно,
Замечание 5. Многочлены (I) и (II) различаются лишь формой записи. Действительно, раскрывая скобки и приводя подобные члены, получаем 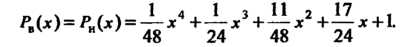
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
| < Предыдущая | Следующая > |
|---|