30.4. Метод итераций

Если каким-либо способом получено приближенное значение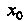Корня уравнения (30.1), то уточнение корня можно осуществить методом последовательных приближений или методом итераций. Для этого уравнение (30.1) представляют в виде

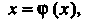(30.10)

Что всегда можно сделать и притом многими способами, например

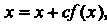(30.11)

Где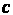— произвольная постоянная.

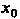Пусть числоЕсть результат подстановкиВ правую часть уравнения

(30.10):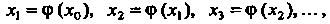

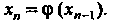(30.12)

Процесс последовательного вычисления чисел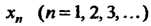По формуле

(30.12) называется методом последовательных приближений или методом итераций. Процесс итераций сходится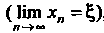, если выполнено условие

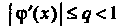(30.13)

На отрезке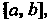Содержащем корень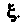

Пример 30.4. Методом итераций найти действительный корень уравнения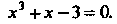

Корень этого уравнения принадлежит отрезку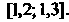Данное уравнение

Можно записать так: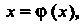Где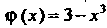; однако этим представлением

Пользоваться нельзя, поскольку т. е. не выполнено условие (30.13).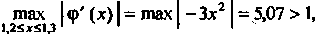

В соответствии с формулой (30.11) получаем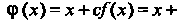

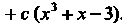Условие (30.13) будет выполнено, например при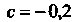

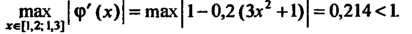
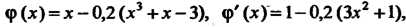
Взяв в качестве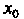Любое значение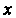Из отрезкаНапример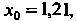

Проведем вычисления по формул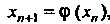еГде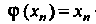

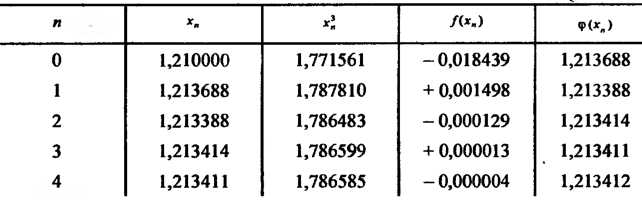
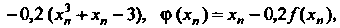И представим их в табл. 30.2, из которой видно, что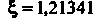- корень уравнения.

Таблица 30.2

< Предыдущая		Следующая >