30.3. Метод касательных

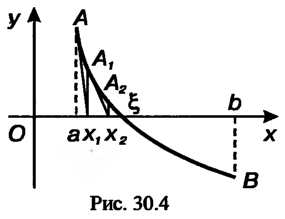
Метод касательных (или метод Ньютона) отличается от метода хорд тем, что здесь рассматривается не секущая, соединяющая концы дуги графика, а касательная к графику. Точка пересечения касательно с осью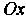Дает приближенное знаг чение корня (рис. 30.4).

В методе касательных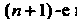Приближение вычисляется по формуле

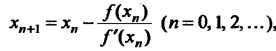, (30.8)

В которой за нулевое приближение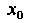Принимается такое значение из отрезка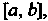Для которого выполняется условие

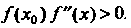(30.9)

Оценка погрешности, как и в методе хорд,

Определяется формулой (30.7).

Пример 30.3. Методом касательных найти действительный корень уравнения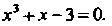

В данном случае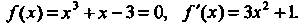Отделив корень уравне

Ния, видим, что он принадлежит отрезку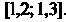, В качестве начального прибли

Жения возьмем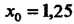(середину этого отрезка); в точке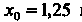Выполняется

Условие (30.9), так как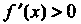И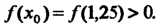Результаты вычислений,

Выполненных по формуле (30.8), заносим в табл. 30.1, из которой видно, что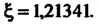

Таблица 30.1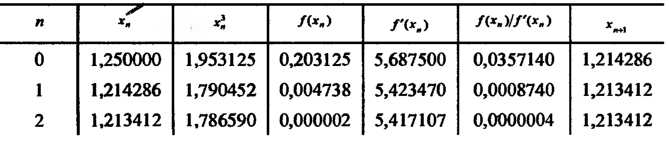

< Предыдущая		Следующая >