30.2. Метод хорд

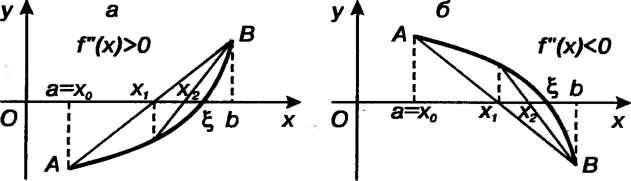
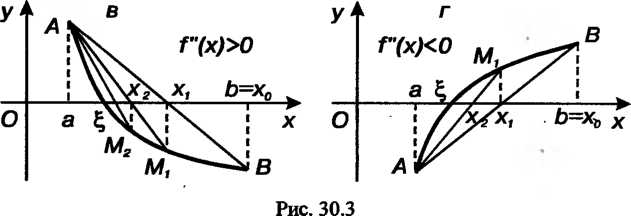
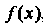Метод хорд, или метод секущих, приближенного решения уравнения (ЗОЛ) имеет следующую геометрическую иллюстрацию: вместо точки пересечения осиИ графика функции, входящей в это уравнение, рассматривается точка пересечения данной оси и отрезка прямой, соединяющей концы дуги графика (рис. 30.3).

Если известно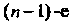Приближение, то я-е вычисляется по формуле

Или по формуле

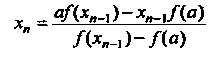(30.5)

В случае (рис. 30.3, в, г), когда

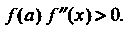(30.6)

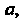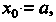В первом случае за начальное приближение принимаетсяТ. е.Во

Втором -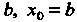(см. рис. 30.3).

Последовательность чисел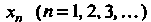Сходится к корню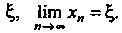

Вычисления приближенийСледует производить до тех пор, пока два

Последовательных приближения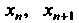Не совпадут на заданное число знаков.-

Для промежуточных выкладок надлежит брать один-два запасных знака.

Оценка абсолютной погрешности определяется формулой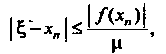  

(30.7)

Пример 30.2. Методом хорд найти действительный корень уравнения

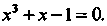
В данном случае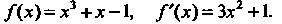Поскольку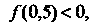

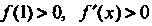Для всех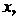То на отрезке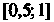Находится единственный дей

Ствительный корень уравнения. Так какТ. е. выполне

Но неравенство (30.4), то пользуемся формулой (30.3), положив в ней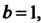

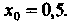Вычислим сначала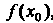,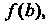Входящие в эту формулу:

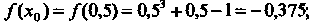
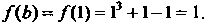По формуле

(30.3), полагая и = 1,2, вычисляем

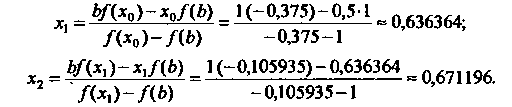
Аналогично вычисляем последующие приближения: '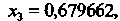

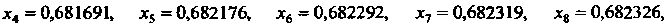
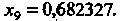Следовательно, с точностью до 0,0001 получено значение

Корня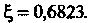

< Предыдущая		Следующая >