30.1. Отделение корней уравнения
Корнем уравнения
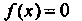(30.1)
Называется такое значение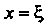
Аргумента функции
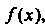При котором это
Уравнение обращается в тождество: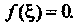
Корень уравнения (30.1) геометри
Чески представляет собой абсциссу точки пересечения, касания или другой общей точки графика функции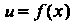
И оси
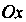(рис. 30.1, а - в).
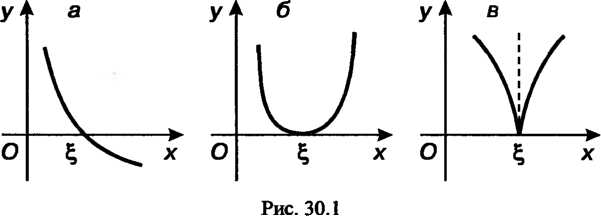
Отделить корень уравнения — значит найти такой конечный промежуток, внутри которого имеется единственный корень данного уравнения. Отделение корней уравнения (30.1) можно выполнить графически, построив график функции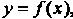 
, по которому можно судить о том, в каких промежутках находятся точки пересечения его с осью
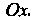В некоторых случаях целесообразно представить уравнение (30.1) в эквивалентном виде:
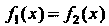(30.2)
С таким расчетом, чтобы графики функций
И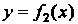
Строились по
Возможности проще. Корень уравнения (30.2) представляет собой абсциссу точки пересечения графиков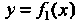
И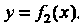
. Таким способом можно, например,
Прямой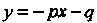
И линии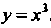
Для отделения корней уравнения (30.1) применяют следующий критерий: если на отрезке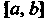
Функции
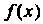Непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки, то на этом отрезке имеется один и только один корень уравнения. Достаточным признаком монотонности функции
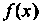На от
Резке является сохранение знака ее первой производной (если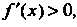
То функ
Ция возрастает; если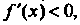
Функция убывает).
Пример 30.1. Отделить корни уравнения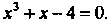
В данном случае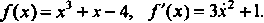
Так как
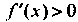При всех
,
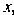То функция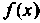
Возрастает в промежутке
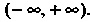Корень считается отделенным,,
Если указан конечный промежуток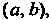
На котором он находится. Методом проб
Находим отрезок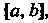
, для которого
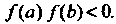Для этого вычислим значения
Функции при некоторых значениях аргумента: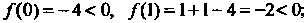
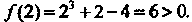Поскольку
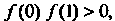То на отрезке
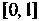Корня нет, так
Как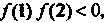
То корень уравнения находится на отрезке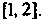
Замечание 1. Можно указать отрезок меньшей длины, которому принадлежит корень. Взяв середину отрезка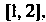
Т. е. положив
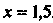, получим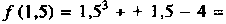
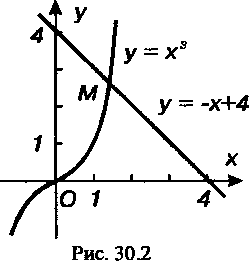
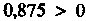; значит, корень находится на отрезке 
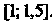, Этот процесс можно продолжать. Замечание 2. Корень данного уравнения можно отделить и графически. Придадим уравнению вид
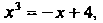Т. е. вид (30.2), и
Построим графики функций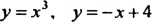
(рис. 30.2). Эти графики пересекаются в точке
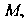абсцисса которой принадлежит интервалу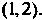
| < Предыдущая | Следующая > |
|---|
