29.12. Тензорное поле
Если каждой точке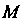
Области
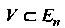Поставлен в соответствие тензор од
Ного и того же типа, то говорят, что в области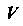
Задано тензорное поле. При переходе от одной системы координат
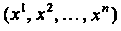К другой
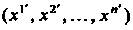Базисные векторы преобразуются следующим образом :
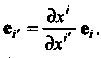Поле тензора валентности
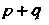Определяется в каждой системе
Координат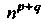
Функциями точки
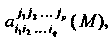Которые при переходе к дру
Гой системе координат преобразуются по закону
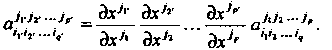
Чтобы определить изменение тензора при переходе от одной точки к другой, надо учитывать не только изменение компонент тензора, но и изменение локального базиса. Например, для контравариантного векторного поля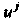
Приращение
Слагаемое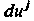
В (29.21) учитывает зависимость координат приращения тензора от приращения его координат, а слагаемое
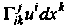Учитывает зависимость - компонент
Приращения тензора от изменения системы координат при переходе от точки к точке.
Вектор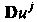
Называют ковариантным или абсолютным дифференциалом векторного поля. Ковариантной или абсолютной производной этого поля называют совокупность величин
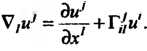
Аналогично вводят ковариантную производную ковариантного векторного поля
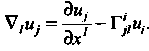
Для тензорного поля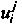
Ковариантная производная вычисляется по формуле
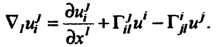
Векторного поля (с точностью до бесконечно малых высшего порядка) равно
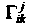- символы Кристоффеля:
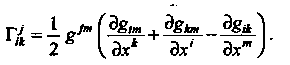
Так же определяется ковариантная производная для тензорного поля любой структуры. Ковариантная производная тензорного поля - тензорное поле, ковариантная валентность которого на единицу выше исходного поля.
Абсолютный дифференциал любого тензорного поля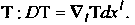
В прямоугольных системах координат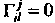
И ковариантное дифференциро
Вание переходит в обычное.
Ковариантное дифференцирование перестановочно со свертыванием Правила ковариантного дифференцирования для суммы и произведения тензоров совпадают с правилами обычного дифференцирования.
ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
| < Предыдущая | Следующая > |
|---|
