29.11. Тензоры в евклидовом пространстве
В евклидовом пространстве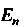 Введено скалярное произведение двух векторов - билинейная форма Иначе говоря, евклидово пространство - это линейное пространство, в котором определен тензор типа
Введено скалярное произведение двух векторов - билинейная форма Иначе говоря, евклидово пространство - это линейное пространство, в котором определен тензор типа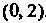 . Если
. Если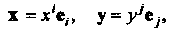 То
То
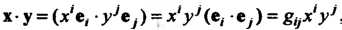 , где
, где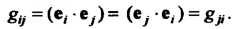 Сим
Сим
Метричный тензор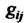 Называют метрическим. В результате свертывания тензоров
Называют метрическим. В результате свертывания тензоров 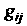 И
И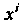 Получают числа— ковариантные координаты вектора
Получают числа— ковариантные координаты вектора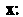
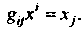 Кова-
Кова-
Риакгные координаты - это проекции вектора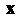 На базисные векторы, так как
На базисные векторы, так как
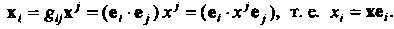 Дважды контравариантный тензор
Дважды контравариантный тензор С матрицей, обратной матрице тензора
С матрицей, обратной матрице тензора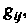 , называют контравариантным метрическим тензором. Любой одновалентный ковариантный тензор
, называют контравариантным метрическим тензором. Любой одновалентный ковариантный тензор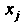 Путем свертывания с тензором
Путем свертывания с тензором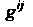 Можно преобразовать в контравариантный
Можно преобразовать в контравариантный
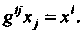 Операцию перехода от контравариантных координат вектора к его
Операцию перехода от контравариантных координат вектора к его
Ковариантным координатам называют операцией «опускания индекса», а операцию перехода от ковариантных координат к контравариантным - операцией «поднятия индекса». Операцию опускания или поднятия индекса в евклидовом пространстве применяют к тензорам любой структуры.
Если базис ортонормирован, то нет необходимости различать ковариантные и контравариантные тензоры, так как матрица (29.16) получена в этом случае транспонированием матрицы (29.13) и во всех преобразованиях участвуют лишь элементы матрицы (29.13). В этом базисе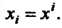
Примером двухвалентного тензора является тензор деформации, который определяет положение точек тела после деформации по отношению к их положению до деформации. Если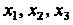 - декартовы прямоугольные координаты точки
- декартовы прямоугольные координаты точки
Тела до деформации,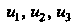 - координаты вектора перемещения и деформация
- координаты вектора перемещения и деформация
Мала, то координаты тензора деформации имеют вид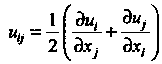
И матрица этого тензора
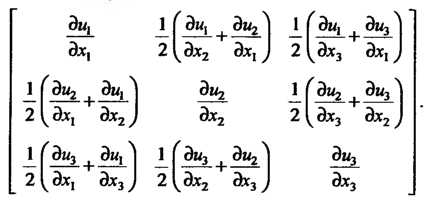
| < Предыдущая | Следующая > |
|---|