29.10. Действия над тензорами
Пусть заданы два тензора одинакового строения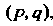 Т. е. заданы координа
Т. е. заданы координа
Ты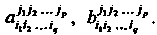 Их суммой будет тензор того же строения с координатами
Их суммой будет тензор того же строения с координатами
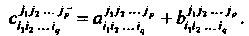
Сказанное остается в силе и при сложении нескольких тензоров одинакового строения.
Если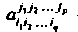 - координаты тензора типа
- координаты тензора типа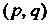 И
И - координаты
- координаты
Тензора типа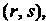 То произведением этих тензоров будет тензор, координаты
То произведением этих тензоров будет тензор, координаты
Которого выражаются следующим образом:
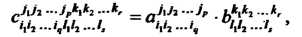
Т. е. в каждом базисе каждую координату первого тензора умножают на каждую координату второго тензора и полученные произведения принимают за координаты нового тензора типа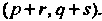 Указанным способом можно перемножать любое число тензоров. Результат умножения зависит не только от типа сомножителей, но и от их порядка.
Указанным способом можно перемножать любое число тензоров. Результат умножения зависит не только от типа сомножителей, но и от их порядка.
Операция свертывания тензора имеет специфически тензорный характер, и применяется к тензорам смешанного типа Пусть дан произвольный тензор, имеющий хотя бы один верхний и хотя бы один нижний индексы. Индексы выбирают произвольно и отбирают те координаты тензора, для которых выбранные индексы имеют одинаковые значения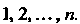 Это означает, что производится
Это означает, что производится
Суммирование всех выбранных координат при фиксированных значениях остальных индексов. Получаем тензор, утративший по сравнению с исходным по одному нижнему и верхнему индексу. Если тип исходного тензора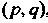 , то полученный
, то полученный
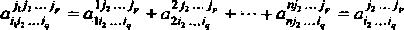
В связи с тем, что валентность тензора при свертывании понижается на две единицы, эта операция является весьма важным источником получения инвариантов - величин, не зависящих от выбора базиса. Если у тензора одинаковое число верхних и нижних индексов, то, применяя операцию свертывания столько раз, сколько верхних или нижних индексов, получают число. При сворачивании тензора типа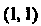 Получаем
Получаем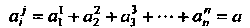 - след соответствующей матрицы. Особенно часто применяется свертывание к тензорам, полученным как произведение. Так, запись линейной формы
- след соответствующей матрицы. Особенно часто применяется свертывание к тензорам, полученным как произведение. Так, запись линейной формы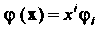 Можно рассматривать как
Можно рассматривать как
Тензор имеет тип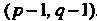 . Пусть
. Пусть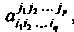 , выбираем, например, индексы
, выбираем, например, индексы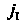 И
И
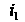 И рассматриваем
И рассматриваем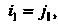 Т. е.
Т. е.
Получение инварианта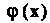 Путем свертывания произведения тензоров
Путем свертывания произведения тензоров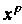 И
И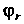 Транспонирование тензоров (операция подстановки индексов) по двум ковариантным или двум контравариантным индексам - преобразование рассматриваемого тензора в тензор того же типа, координаты которого отличаются от координат исходного тензора порядком транспонируемых индексов. Например,
Транспонирование тензоров (операция подстановки индексов) по двум ковариантным или двум контравариантным индексам - преобразование рассматриваемого тензора в тензор того же типа, координаты которого отличаются от координат исходного тензора порядком транспонируемых индексов. Например,
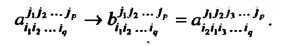
Операция симметрирования по группе р ковариантных или контравариантных индексов заключается в следующем: транспонируют тензор, совершая всевозможные перестановки индексов выбранной группы. Полученные таким образом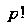 тензоров складывают и делят эту сумму на
тензоров складывают и делят эту сумму на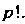 Полученный тензор обозначается заключением выбранной группы индексов в круглые скобки. Так, тензор
Полученный тензор обозначается заключением выбранной группы индексов в круглые скобки. Так, тензор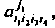 симметрированный по индексам
симметрированный по индексам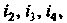 Имеет вид
Имеет вид
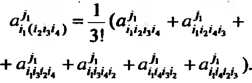
Операция альтернирования (альтернации) по группе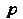 Ковариантных или контравариантных индексов производится следующим образом: транспонируем тензор, совершая всевозможные перестановки индексов выбранной группы. Получаем
Ковариантных или контравариантных индексов производится следующим образом: транспонируем тензор, совершая всевозможные перестановки индексов выбранной группы. Получаем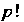 Тензоров. Далее складываем тензоры, полученные четными перестановками и из этого результата вычитаем тензоры, полученные нечетными перестановками, окончательный результат делим на
Тензоров. Далее складываем тензоры, полученные четными перестановками и из этого результата вычитаем тензоры, полученные нечетными перестановками, окончательный результат делим на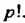 Полученный тензор обозначается заключением выбранной группы индексов в квадратные скобки. В результате альтернирования тензора
Полученный тензор обозначается заключением выбранной группы индексов в квадратные скобки. В результате альтернирования тензора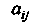 Получаем
Получаем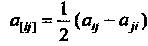 Альтернирование тензора
Альтернирование тензора
 По индексам
По индексам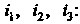
Тензор называют кососимметрическим по нескольким одноименным индексам, если он умножается на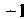 При транспонировании любых двух из этих индексов. Примером кососимметрического тензора может быть тензор типа
При транспонировании любых двух из этих индексов. Примером кососимметрического тензора может быть тензор типа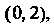 Координат
Координат
Ты которого образуют кососимметрическую матрицу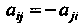 , т. е. матрицу вида
, т. е. матрицу вида
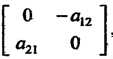 , или тензор типа
, или тензор типа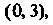 Координаты которого обладают свойством
Координаты которого обладают свойством
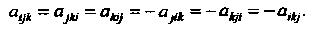
В результате альтернирования получают кососимметрический тензор по индексам, участвующим в альтернации.
| < Предыдущая | Следующая > |
|---|