29.09. Полилинейные функции векторного аргумента. Понятие тензора
Если каждому вектору Из
Из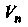 Поставлено в соответствие число
Поставлено в соответствие число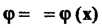 так, что для любых векторов
так, что для любых векторов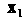 И
И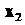 Из
Из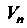
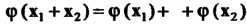 И для
И для
Любого числа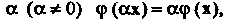 То
То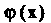 Называют линейной функцией
Называют линейной функцией
Или линейной формой.
Обозначая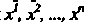 Координаты вектора
Координаты вектора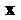 В базисе
В базисе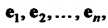 Получаем
Получаем
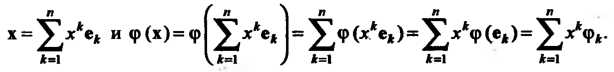
Числа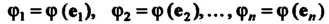 Называют коэффициентами линей
Называют коэффициентами линей
Ной формы. Линейную форму считают заданной, если в некотором базисе заданы ее коэффициенты.
Если любым векторам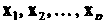 Из
Из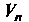 Поставлено в соответствие число
Поставлено в соответствие число
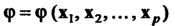 Так, что
Так, что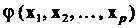 — функция линейная относитель
— функция линейная относитель
Но всех своих аргументов, то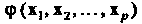 Называют полилинейной функцией
Называют полилинейной функцией
Или полилинейной формой.
В этом случае при
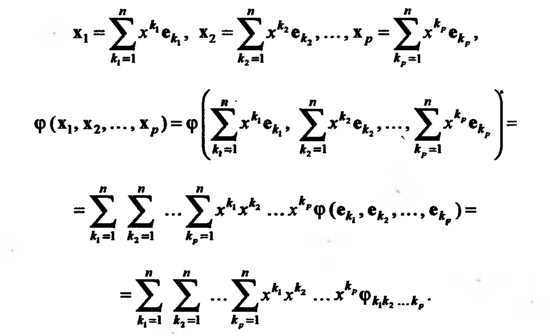
Числа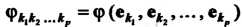 Называют коэффициентами полилинейной
Называют коэффициентами полилинейной
Формы. Всего их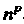 . При
. При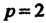 Форму называют билинейной.
Форму называют билинейной.
В тензорном исчислении принято соглашение о суммировании: если в некотором одночленном выражении одинаковый буквенный индекс встречается
Дважды - один раз вверху и один раз внизу, то это означает сумму выражений этого рода для значений индекса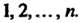 Например,
Например,

Обозначение индексов суммирования не играет роли: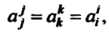
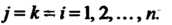
Если в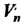 Выбраны два базиса
Выбраны два базиса
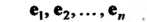 (29.12)
(29.12)
И
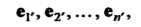 (29.13)
(29.13)
То каждый вектор системы (29.13) можно разложить по базису (29.12):
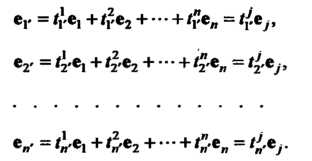 (29.14)
(29.14)
Матрица перехода от базиса (29.12) к базису (29.13) имеет вид
 (29.15)
(29.15)
Матрица перехода от базиса (29.13) к базису (29.12) является обратной матрице (29.15):
 (29.16)
(29.16)
Учитывая соглашение о суммировании, формулы (29.14) можно записать в виде
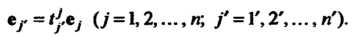 (29.17)
(29.17)
Аналогично, учитывая матрицу (29.16) и соглашение о суммировании, получаем
Преобразования, в которых участвуют элементы матрицы (29.15), называют ковариантными (сопреобразующимися, изменяющимися так же). Преобразования, с участием элементов матрицы (29.16), называют контравариантными (противопреобразукмцимися).
Ковариантным тензором ранга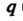 (тензором типа
(тензором типа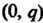 Или
Или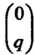 ) называется величина, которая в каждом базисе векторного пространства
) называется величина, которая в каждом базисе векторного пространства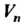 Задается
Задается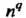 Упорядоченными системами чисел
Упорядоченными системами чисел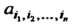 В базисе (29.12) и
В базисе (29.12) и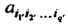 В базисе (29.13)). которые при переходе от базиса (29.12) к базису (29.13) преобразуются по закону
В базисе (29.13)). которые при переходе от базиса (29.12) к базису (29.13) преобразуются по закону
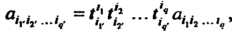 (29.19)
(29.19)
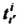 - элементы матрицы (29.15). Ранг тензора называют также валентностью. Пусть
- элементы матрицы (29.15). Ранг тензора называют также валентностью. Пусть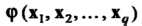 - линейная форма порядка
- линейная форма порядка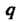 С коэффициентами
С коэффициентами
(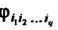 В базисе (29.12) и
В базисе (29.12) и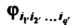 В базисе (29.13). Учитывая определение коэф
В базисе (29.13). Учитывая определение коэф
Фициентов полилинейной формы, соотношение (29.17) и свойства линейности, можно получить
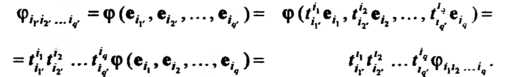
Таким образом, линейная форма порядка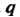 Является ковариантным тензором типа
Является ковариантным тензором типа 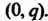 Удобно считать, что и тензор типа
Удобно считать, что и тензор типа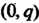 Является линейной формой порядка
Является линейной формой порядка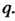
Контравариантным тензором ранга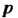 (тензором типа
(тензором типа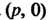 Или
Или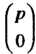 ) называется
) называется
Величина, которая в каждом базисе-векторного пространства Задается
Задается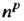 Упорядоченными системами чисел
Упорядоченными системами чисел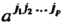 В базисе (29.12) и
В базисе (29.12) и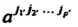 В базисе (29.13)), которые при переходе от базиса (29.12) к базису (29.13) преобразуются по закону
В базисе (29.13)), которые при переходе от базиса (29.12) к базису (29.13) преобразуются по закону
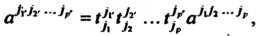 (29.20)
(29.20)
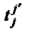 - элементы матрицы (29.16).
- элементы матрицы (29.16).
Если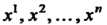 Координаты вектора
Координаты вектора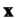 В базисе (29.12),
В базисе (29.12),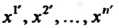 -в
-в
Базисе (29.13), то Следовательно,
Следовательно,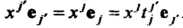
Приравнивая координаты при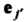 , получаем
, получаем
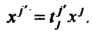
Таким образом, вектор - это контравариантный тензор, т. е. тензор типа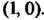 Наоборот, тензор типа
Наоборот, тензор типа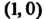 Можно рассматривать как вектор.
Можно рассматривать как вектор.
Числа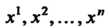 Называют контравариантными координатами вектора.
Называют контравариантными координатами вектора.
Тензором типа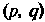 (
(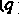 Раз ковариангным и
Раз ковариангным и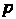 Раз контравариантным) называется величина, которая в каждом базисе векторного пространства
Раз контравариантным) называется величина, которая в каждом базисе векторного пространства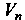 Задается
Задается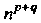 Упорядоченными системами чисел (
Упорядоченными системами чисел (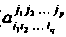 В базисе (29.12) и
В базисе (29.12) и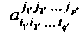 В базисе (29.13)), которые при переходе от базиса (29.12) к базису (29.13) преобразуется по закону
В базисе (29.13)), которые при переходе от базиса (29.12) к базису (29.13) преобразуется по закону
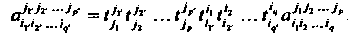
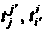 - элементы матриц (29.15) и (29.16). Числа
- элементы матриц (29.15) и (29.16). Числа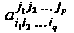 Называют координатами
Называют координатами
Тензора в базисе (29.12),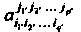 - координатами тензора в базисе (29.13).
- координатами тензора в базисе (29.13).
| < Предыдущая | Следующая > |
|---|