29.08. Оператор Гамильтона. Операции второго порядка в векторном анализе. Оператор Лапласа
Оператор Гамильтона (оператор набла) - линейный дифференциальный оператор по определению записывают в виде
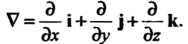
С учетом этого оператора основные операции теории поля можно записать так:
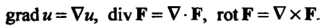
С помощью оператора набла удобно получать и записывать различные формулы векторного анализа, причем эти формулы приобретают в такой записи большую наглядность и выразительность. При выполнении действий с оператором
Следует учитывать, что это оператор дифференциальный и векторный, т. е. пользоваться правилами дифференциального исчисления и векторной алгебры. При этом следует помнить, что, если
Действует на какое-либо произведение, то в первую очередь учитывают его дифференциальные свойства, а затем векторные. Входящие в состав формулы величины, которые подвергаются воздействию оператора набла, обозначают стрелкой, в окончательном результате они должны стоять слева от него. Рассмотрим операцию взятия дивергенции от векторного произведения поле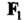й
И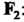
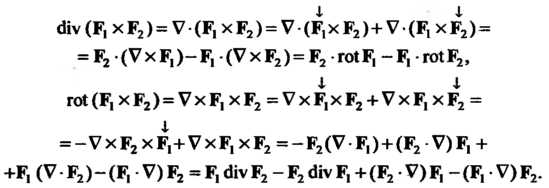
Здесь была использована формула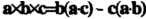
. С использованием последней получим
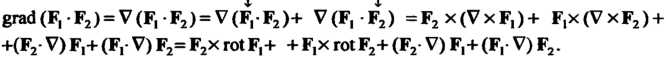
Если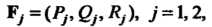
То
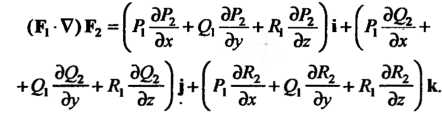
Эту операцию можно рассматривать как результат применения операции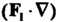 
К каждой составляющей вектора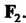
Попарные комбинации операций градиента дивергенции и ротора называют операциями второго порядка. Применительно к скалярному полю имеют смысл две операци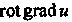и
И
I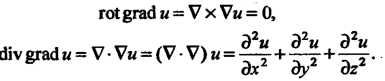
Символ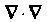
Называют оператором Лапласа и обозначают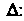
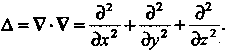
Применительно к векторной величине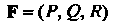
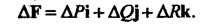В криволинейных ортогональных координатах
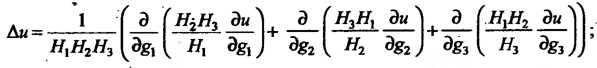
В цилиндрических координатах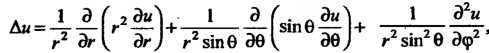 
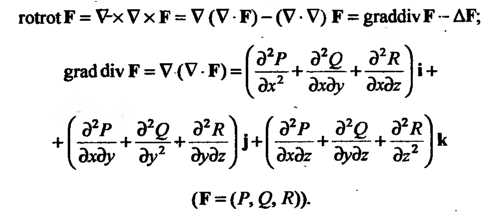
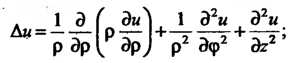в сферических координатах
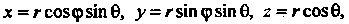
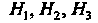- параметры Ламе
(см. формулы (29.6)).
Операции второго порядка для векторного поля:
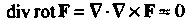- поле, являющееся ротором некоторого поля
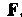соленоидально; .ч
| < Предыдущая | Следующая > |
|---|
