29.07. Потенциальное поле

 

Пусть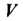— односвязная область, в которой задано поле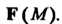

Векторное поле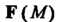Называется потенциальным, если его можно предста

Вить в виде градиента некоторого скалярного поля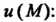

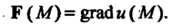
Поле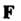Потенциально в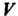Тогда и только тогда, когда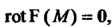Т. е.

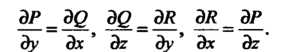
Это условия (21.16). При непрерывных _ со своими частными произ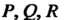 водными задача о нахождении потенциала свелась к задаче восстановления функции по ее полному дифференциалу (см. п. 21.3).

Пример 29.10. Найти потенциал поля

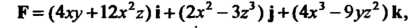
Если он существует.

Исследуем потенциальность поля:

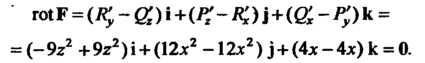
ПолеПотенциально. Так как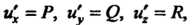То получаем

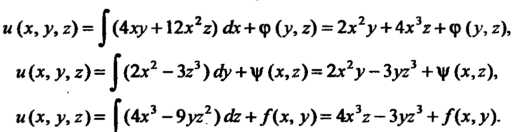
Следовательно,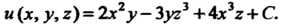

< Предыдущая		Следующая >