29.06.  Ротор векторного поля. Теорема Стокса

 

Ротором (вихрем) поля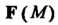В точке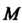Называется

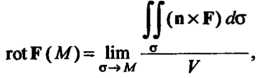
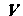
Если этот предел существует. Здесь. — область, ограниченная замкнутой гладкой или кусочно-гладкой поверхностью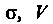— объем области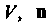- нормаль к поверхности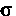В точке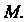

Для декартовой системы координат с непрерывными вместе со своими частными производными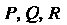

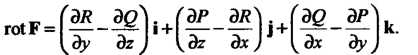(29. II)

В символической форме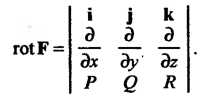 Свойства ротора:

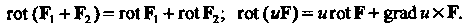
В ортогональных криволинейных координатах

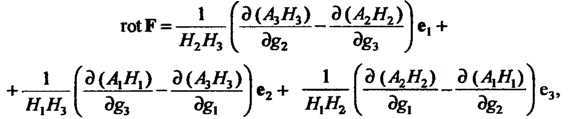
Где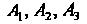- координаты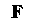В базисе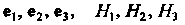- параметры

Ламе (см. формулы (29.-6)); в цилиндрических координатах

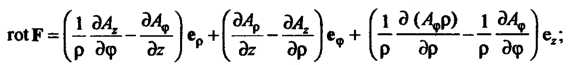
В сферических координатах

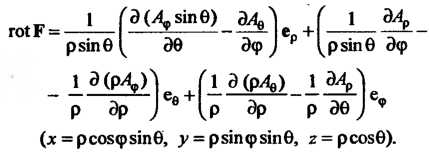
Формула Стокса. Формула (22.11) в векторной форме имеет вид

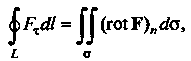
Т. е. циркуляция векторного поля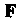Вдоль некоторого замкнутого контура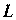Равна потоку ротора этого векторного поля через поверхность, ограниченную этим

Контуром. Из последней формулы

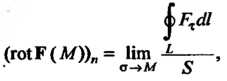
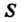- площадь поверхности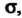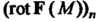- проекция ротора на нормаль.

Пример 29.9. Найти вихрь векторного поля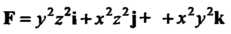 в произвольной точке.

Находим частные производные: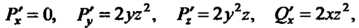

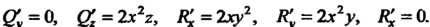По формуле (29.11) имеем

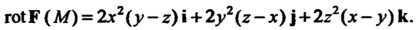
< Предыдущая		Следующая >