29.05.  Циркуляция векторного поля

 

Циркуляцией векторного поля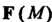Вдоль линии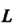Называется криволиней

Ный интеграл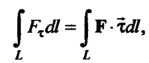

Где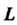— гладкая или кусочно-гладкая линия,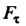- тангенциальная составляющая поля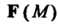На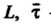- единичный вектор касательной к линии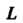В точке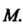

В декартовой системе координат

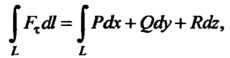
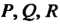- непрерывные составляющие поля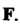Вычисление полученного криволинейного интеграла второго рода описайо в п. 21.2.

Если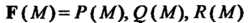— силовое поле, то его циркуляция вдоль

Линии L представляет собой работу этого поля вдоль линии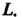 Пример 29.8. Найти работу, производимую силой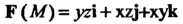

Вдоль линии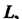. описываемой уравнениями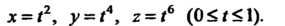

По формуле, выражающей циркуляцию в декартовой системе координат, находим

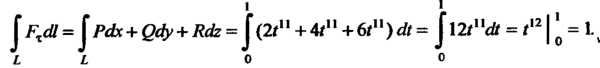
< Предыдущая		Следующая >