29.04. Поток векторного поля через поверхность. Дивергенция. Соленоидальное поле. Теорема Остроградского

 

Потоком векторного поля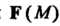Через поверхность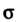В сторону, определяемую

Единичным вектором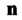Нормали к поверхности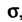, называют интеграл:

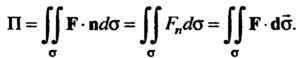
В декартовой системе координат, если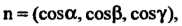То

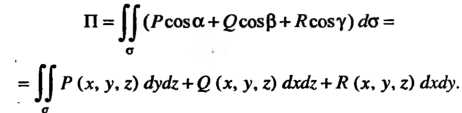
Способы вычисления этого поверхностного интеграла указаны в п. 22.2.

Пусть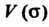- объем области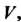Ограниченной замкнутой поверхностью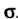. В этом

Случае поток через внешнюю сторону поверхности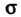Записывают в виде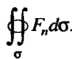

Дивергенцией (расходимостью) векторного поля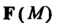В точке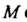Области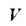

Называется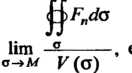;сли такой предел существует. Следовательно,

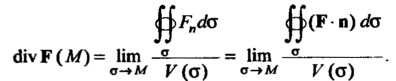
Теорема 29.1. Если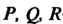Непрерывны вместе со своими частными произ

Водными в области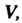То дивергенция поля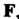Заданного координатами 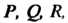существует во всех точках области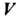И в любой декартовой системе координат выражается формулой

Если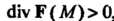, то точка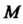- источник векторных линий, если

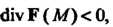То точка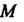- сток силовых линий.

Свойства дивергенции:

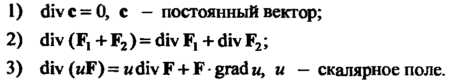
В криволинейных ортогональных координатах

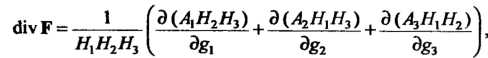
Где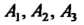- координаты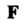В базисе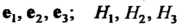- параметры

Ламе, определенные формулой (29.6); в цилиндрических координатах

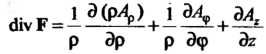
В сферических координатах

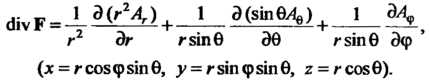
Векторное поле, дивергенция в каждой точке которого равна нулю, называется соленоидальным или трубчатым.

Теорема 29.2 (теорема Остроградского). Формула (22.12) для векторного поля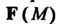Имеет вид

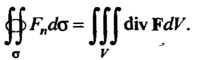(29.10)

Пример 29.6. Найти поток векторного поля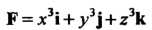Через

Внешнюю сторону поверхности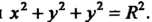

Воспользуемся формулой (29.10), выражающейпоток векторного поля через

Тройной интеграл. Так как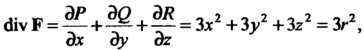То по

Формуле (29.10) имеем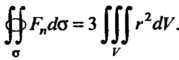Введя сферические координаты

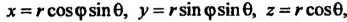Вычислим тройной интеграл:

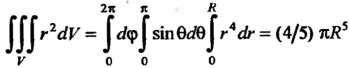
Следовательно,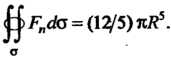

Пример 29.7. Найтидивергенцию векторного поля

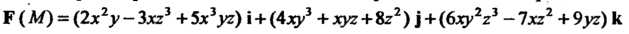В

Точке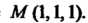

Вычислим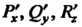В точке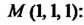

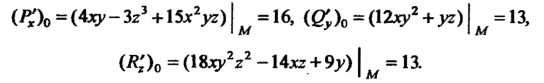
Подставляя полученные значения в формулу (29.9), получаем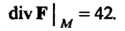

< Предыдущая		Следующая >