29.03. Векторное поле. Векторные линии

 

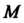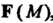Если каждой точкеОбластиПоставлен в соответствие некоторый вектор , то говорят, что вЗадано векторное поле.

В декартовой системе координат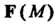Можно представить совокупностью

Трех скалярных функций, являющихся координатами вектора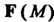. Обозначим

Их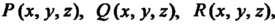Тогда

Иногда векторные поля обладают специальными свойствами симметрии.

Векторное поле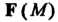Называют одномерным, если существует декартова сис

Тема координат такая, что координаты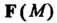Имеют вид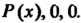

Если существует такая цилиндрическая система координат, что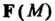Зависит

От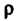И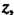Но не зависит от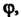То поле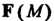Называют осесимметрическим. Если

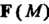| зависит лишь от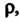То поле называют цилиндрическим.

Векторное поле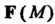Называют плоскопараллельным, если существует де

Картова система координат такая, что координаты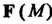I можно задать функция

Ми двух переменных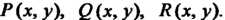

Векторной линией (силовой линией, линией тока) векторного поля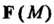На

Зывается линия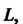Лежащая в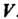, если в каждой точке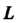Направление касательной к ней совпадает с направлением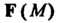В этой точке.

Параметрическое дифференциальное уравнение векторной линии, проходящей через точку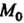, выражается формулами

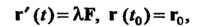
Где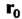— радиус-вектор начальной точки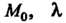— произвольное число,-

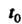Начальное значение параметра,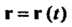- уравнение векторной линии.

Система дифференциальных уравнений векторных линий

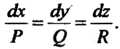(29.8)

При непрерывно дифференцируемых функциях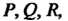Ни в одной точке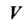

Не обращающихся одновременно в нуль, через каждую точку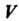Пройдет единственная векторная линия.

Часть пространства, в котором задано векторное поле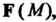Ограниченное неко

Торой поверхностью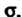, называется векторной трубкой, если в каждой точке поверхности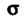Нормаль к ней ортогональна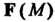В этой же точке, т. е. векторная трубка - часть пространства, состоящая из целых векторных линий, каждая из которых или целиком лежит внутри векторной трубки или целиком находящаяся вне ее.

Пример 29.5. Найти векторные линии векторного поля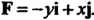 Система (29.8), из которой находятся векторные линии, в данном случае имеет

Вид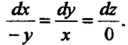Эту систему уравнений можно записать так: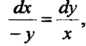

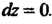Из этих уравнений находим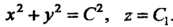Эти уравнения опреде

Ляют векторные линии — окружности в плоскости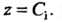

< Предыдущая		Следующая >