29.02. Градиент скалярного поля. Производная по направлению

Линейной формой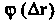Относительно вектора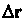Называют скалярное произведе

Ние вектора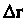На некоторый вектор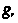Не зависящий от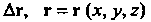-радиус-

Вектор точки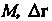- вектор, соединяющий точки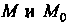

Скалярное поле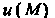Называется дифференцируемым в точкеИз области

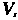Если приращение поля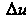В этой точке можно представить в виде

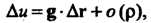(29.3)

Где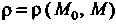- расстояние между точками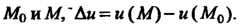

Градиентом дифференцируемого в точке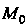Скалярного поля называют вектор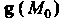Из (29.3). Обозначение: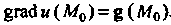

Если поле дифференцируемо в каждой точке области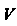, то оно дифференцируемо в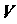. В этом случае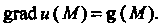

При заданной декартовой системе координат

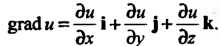
Свойства градиента:

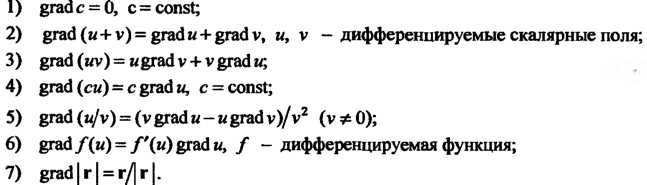
Если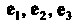- базис в ортогональной криволинейной системе координат

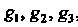, то

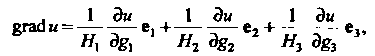
Где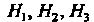- параметры Ламе, определенные формулой

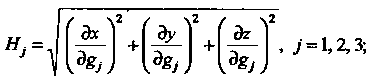(29.6)

В цилиндрической системе координат 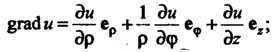 в сферической системе координат

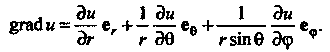
Дифференциалом скалярного поля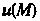Называют скалярное произведение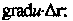

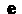
Пусть _ - единичный вектор, указывающий направление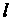В точке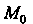Области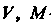- произвольная точка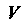, отличная от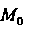И такая, что вектор 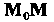коллинеарен вектору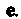

Предел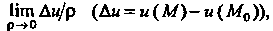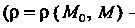- расстояние между

Точками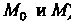I, если он существует, называют производной поля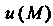В точ

Ке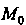По направлению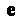И обозначают символом

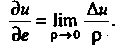
Где

4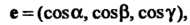

ИЛИ

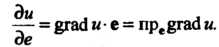
Если е имеет направление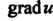, то

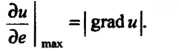
Пример 29.3. Найти величину и направление градиента скалярного поля 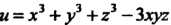В точке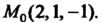

Находим частные производные функции к 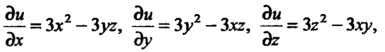 их значения в точке:

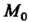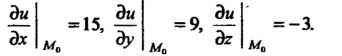
По формуле (29.4) получаем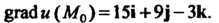

Величину градиента находим по формуле (29.5):

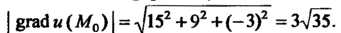
Пример 29.4. Найти производную поля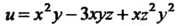В точке

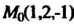По направлению вектора iОбразующего с координатными осями острые углы 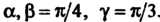Установить характер изменения поля в данном направлении. Частные производные функции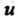В точке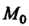Имеют значения:

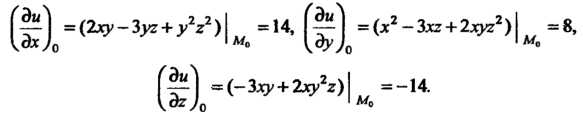
По условию задачи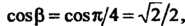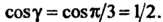Поскольку

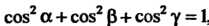, а угол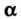- острый, т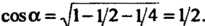о. По

Формуле (29.7) находим

Так как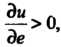Скалярное поле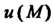Возрастает в данном направлении.

< Предыдущая		Следующая >