28.2. Линейные дифференциальные уравнения с частными производными первого порядка

Дифференциальное уравнение с частными производными первого порядка от функции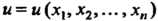В общем виде можно записать так:

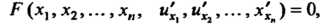(28.1)

Где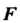- заданная функция своих аргументов.

Линейным однородным дифференциальным уравнением с частными производными первого порядка называется уравнение вида

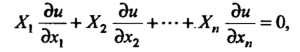(28.2)

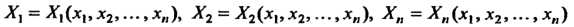(28.3)

- заданные функции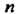Аргументов-

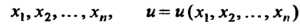Неизвестная функция.

Наряду с уравнением (28.2) рассматривают соответствующую ему систему дифференциальных уравнений в симметрической форме:

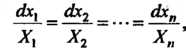(28.4)

В которой функции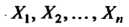Определяются формулами (28.3). Систему

(28.4) можно записать и в нормальной форме:

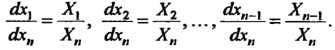(28.5)

Теорема 28.1. Если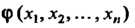- интеграл системы (28.4) или (28.5),

То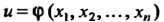— решение уравнения (28.2).

Теорема 28.2. Если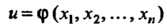- решение уравнения (28.2), то

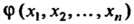- интеграл системы (28.4) или (28.5).

Теорема 28.3. Если

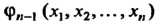— независимые интегралы системы (28.4), то

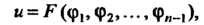(28.6)

Где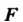— произвольная функция, имеющая непрерывные частные производные по аргументам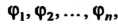Является решением уравнения (28.2).

Линейным неоднородным (или квазилинейным) уравнением с частными производными первого порядка называется уравнение вида

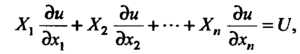(28.7)

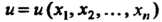— неизвестная функция. Не исключается случай, когда 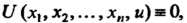Но хотя бы одна из функций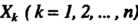I зависит от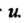

Наряду с уравнением (28.7) рассматривают систему дифференциальных уравнений

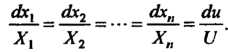(28.9)

Если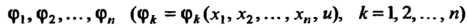- независимые

Интегралы системы (28.9), то

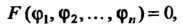(28.10)

Где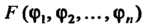- произвольная дифференцируемая функция своих аргу

Ментов, будет решением.

Пример 28.3. Проинтегрировать уравнение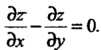

Это уравнение вида (28.2), в котором Записываем систему (28.4) и интегрируем ее:

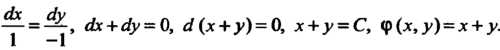
Формула (28.6) принимает ввд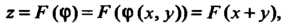

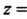
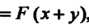, где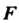— произвольная дифференцируемая функция.

Пример 28.4. Проинтегрировать уравнение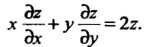

Это уравнение вида (28.7), в котором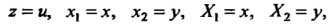

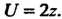Записываем систему (28.9) и интегрируем ее:

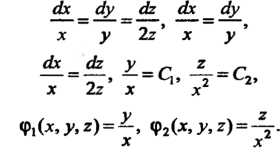
В соответствии с формулой (28.10) получаем решени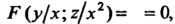е где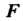— произвольная дифференцируемая функция.

< Предыдущая		Следующая >