28.1. Основные определения

. Дифференциальным уравнением с частными производными называется уравнение относительно неизвестной функции нескольких переменных, ее аргументов и частных производных различных порядков. Если искомая функция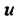Зависит от и переменных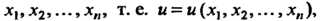То дифференциальное урав

Нение с частными производными имеет вид

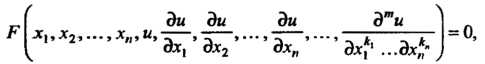
Где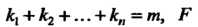- заданная функция.

Порядком дифференциального уравнения с • частными производными называется порядок старшей производной, входящей в это уравнение. Решением дифференциального уравнения с частными производными называется функция, имеющая соответствующие частные производные и обращающая это уравнение в тождество. Проинтегрировать дифференциальное уравнение с частными производными - значит найти все его решения.

Пример 28.1. Проинтегрировать уравнение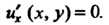 Этому уравнению удовлетворяет любая дифференцируемая функция 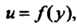зависящая только отТак как

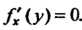
Пример 28.2. Проинтегрировать уравнение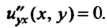 Обозначим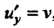, тогда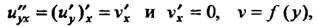Где-

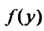Произвольная функция переменной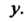ПосколькуТо

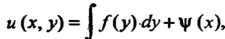Где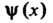— произвольная функция аргумента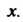

Первое слагаемое последней формулы представляет собой произвольную функцию от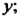Обозначим ее через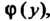Тогда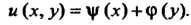 Полученное решение содержит две произвольные функции.

< Предыдущая		Следующая >