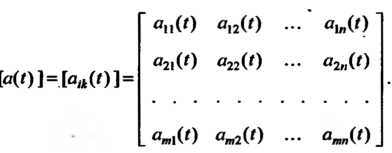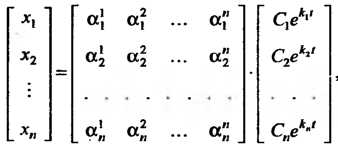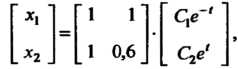27.7. Применение матриц к решению систем дифференциальных уравнений с постоянными коэффициентами

Производная от матрицы. Рассмотрим матрицу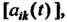Элементами которой

Являются дифференцируемые функции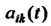Аргумента t:

I

Производной матрицыНазывается матрица, элементы которой являются

Производными соответствующих элементов матрицы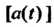

Употребляют следующие символические записи этого равенства:

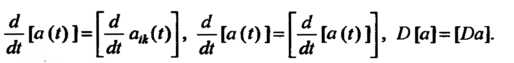
Матричная запись системы дифференциальных уравнений с постоянными коэффициентами и ее решений. Рассмотрим систему п линейных дифференциальных уравнений с искомыми функциями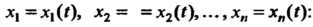

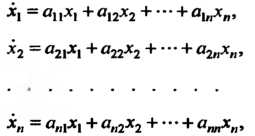(27.27)

Где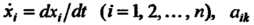- постоянные.

Если

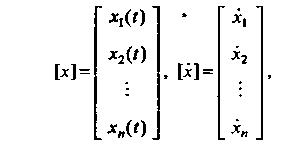
То систему (27.27) в матричной форме можно записать так:

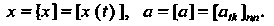
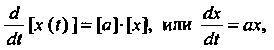
Решение системы (27.27) в матричной форме имеет ввд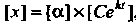, или

О

(27.28)

Где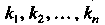— корни характеристического уравнения матрицы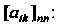  

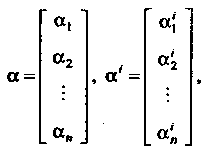
(27.29)

Числа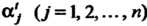I, соответствующие каждому значение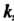, определяются из

Системы уравнени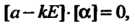йИли

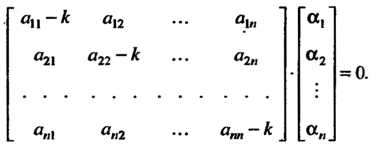(27.30)

Пример 27.11. Записать в матричной форме систему и решение системы линейных дифференциальных уравнений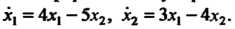 Так как

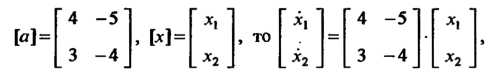
Получена матричная форма данной системы уравнений.

Составляем характеристическое уравнение (по формуле (27.29)) и систему

(27.30) для определения значени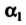йИ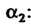

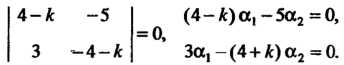
Характеристическое уравнение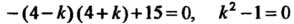Имеет корни

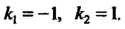Системы уравнений для определения чисел а, и а2 принимают вид

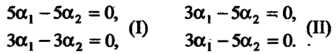
Из системы (I) следует, что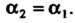Полагая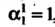, получаем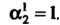Из систе

Мы (II) находим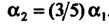. Полагая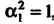, вычисляем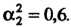В соответст

Вии с (27.28) получаем общее решение системы в матричной форме

S

Или в обычном виде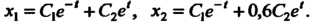

Глава 28

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

< Предыдущая		Следующая >