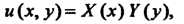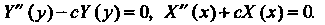28.3. Линейные дифференциальные уравнения с частными производными второго порядка

Уравнение с частными производными второго порядка называется линейным относительно старших производных, если оно содержит эти производные лишь в первой степени.

Линейное дифференциальное уравнение с частными производными второго порядка относительно функции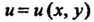Двух переменных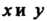Можно записать так:

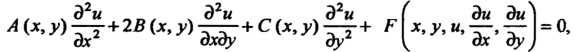
Где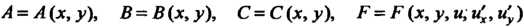- заданные

Функции своих аргументов. Уравнение (28.11) называется уравнением гиперболического типа в данной области, если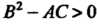В этой области; уравнением параболического типа, если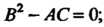Уравнением эллиптического типа, если

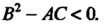Если выражение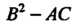В данной области меняет знак, то уравне

Ние (28.11) называется уравнением смешанного типа.

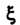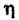Уравнение (28.11) можно привести к каноническому виду переходом к новым переменнымИПо формулам

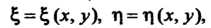(28.12)

Где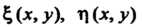- дважды непрерывно дифференцируемые функции аргумен

Тов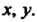Чтобы найти эти функции, рассматривают характеристическое уравнение

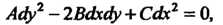(28.13)

Которое равносильно системе двух уравнений

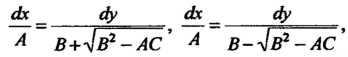(28.14)

Где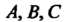Те же, что и в уравнении (28.11).

Интегральные кривые уравнения (28.13), или, что то же самое, уравнений

(28.14), называются характеристиками уравнения (28.11). Если уравнение (28.11) гиперболического типа, то первые интегралы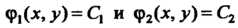Дейст

Вительны и различны. Они определяют два различных семейства действительных характеристик уравнения (28.11). С помощью замены переменных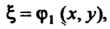

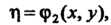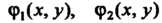Где- интегралы системы (28.14), уравнение

(28.11) приводят к каноническому виду уравнения гиперболического типа:

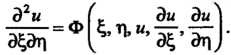
(28.11)

Замечание. Уравнение гиперболического типа с помощью замены переменных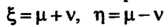Можно привести к другому каноническому виду:

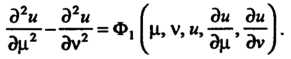
Если уравнение (28.11) параболического типа, то уравнения (28.14) совпадают; в этом случае получают один первый интеграл системы (28.14)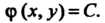Фор

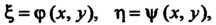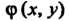Мулы (28.12) принимают видГде- интеграл

Системы (28.14), а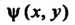- любая функция, удовлетворяющая условию-

Якобиан функци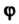йИ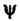Отличен от нуля:

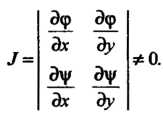(28.15)

Уравнение (28.11) приводят к каноническому виду параболического уравнения:

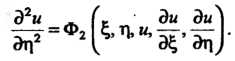
Если уравнение (28.11) эллиптического типа, то первые интегралы системы

(28.14) будут комплексно-сопряженными: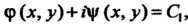

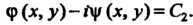С помощью замены переменных по формулам 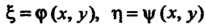Уравнение (28.11) приводят к виду

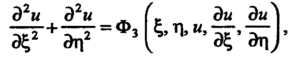
Называемому каноническим видом уравнения эллиптического вида.

Пр имер 28.5. Привести к каноническому виду уравнение

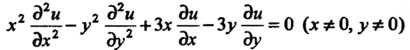
И проинтегрировать его.

Это уравнение гиперболического типа во всех точках плоскости, кроме точек,

Лежащих на осях координат, поскольку для него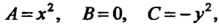

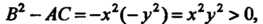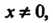
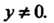ЕслиУравнение характеристик

(28.13) принимает вид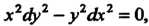Или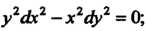Оно равносильно

Двум уравнениям: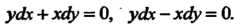Интегрируя эти уравнения, полу

Чаем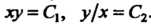. Введем новые переменные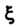И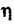По формулам (28.12):

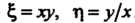. Находим частные производные:

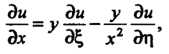
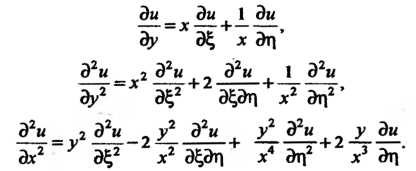
Подставляя эти выражения в исходное уравнение, получаем 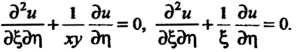 Проинтегрируем уравнениеОбозначим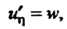Тогда

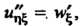
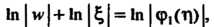
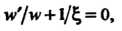'  Л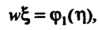

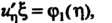
Следовательно,

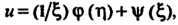ГдеИ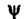- произвольные дважды дифференцируемые функции своих аргументов. Возвращаясь к переменным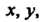Получаем

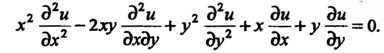
Пример 28.6. Найти общее решение уравнения

Это уравнение параболического типа на всей плоскости Оху, так как для него

Уравнение характеристик

(28.13) принимает вид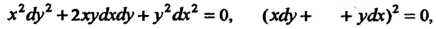

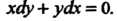Поскольку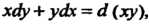То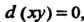Откуда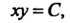

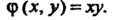В формулах (28.12) положим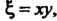А в качестве функции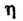Возь

Мем любую функцию, удовлетворяющую условию (28.15), в частности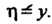 Преобразуем данное уравнение, введя новые переменные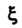И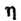По формулам 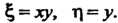Находим выражения для частных производных по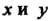Через ча

Стные производные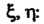

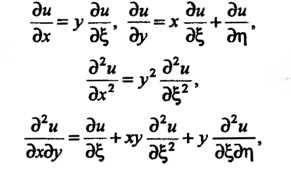
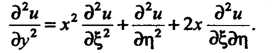
Подставляя эти выражения в исходное уравнение, получаем 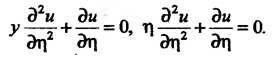 Введем новую функцию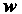По формуле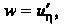Тогда

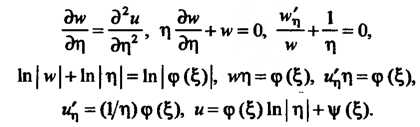
Следовательно, общее решение уравнения определяется формулой 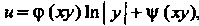, где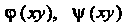- произвольные дважды дифферен

Цируемые функции от произведенияАргументов‘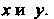

Пример 28.7. Найти решение уравнения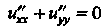В полосе

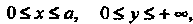Удовлетворяющее условиям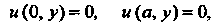

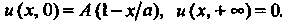
Это каноническое уравнение эллиптического типа. Решение будем искать с помощью метода Фурье (метода разделения переменных). Искомую функцию 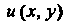Представим в виде произведения

(I)

Где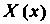- функция только от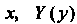— функция только от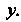Так как

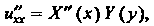
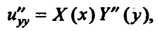То уравнение принимает вид 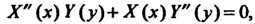Откуда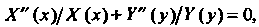Или

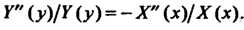Поскольку функция (I) — решение уравнения, то последнее равенство должно выполняться для всех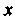И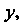Что возможно лишь тогда, когда обе части не зависят ни от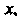. ни от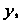Т. е. являются постоянными. Обозначив эту постоянную буквой с, получим два обыкновенных дифференциальных уравнения с постоянными коэффициентами:

(II)

Считая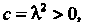Находим решения этих уравнений:

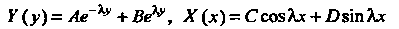
(характеристические уравнения для уравнений (II):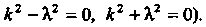

Следовательно, формула (I) примет вид

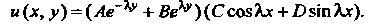
Так как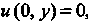, т. е.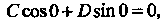То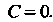Условие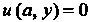При

Водит к равенству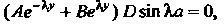Откуда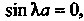

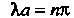
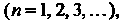
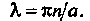Поскольку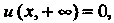Или

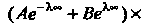
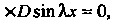То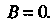Таким образом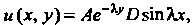Где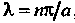, т. е.

Решением является любая функция

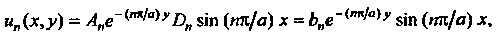
Где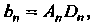, и ряд из этих функций

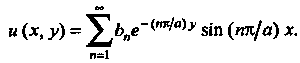
Постоянные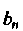Определим так, чтобы выполнялось условие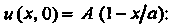

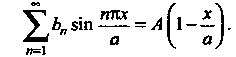
Значит, числаЯвляются коэффициентами ряда Фурье для функции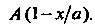 Эти коэффициенты находим по формуле

И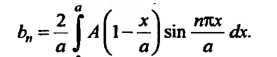

Вычислив интеграл, получим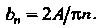

Следовательно, искомое решение определяется формулой

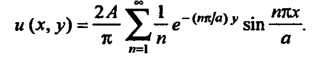
< Предыдущая		Следующая >