27.4. Линейные неоднородные уравнения л-го порядка с постоянными коэффициентами

Рассмотрим линейное неоднородное уравнение я-го порядка с постоянными коэффициентами

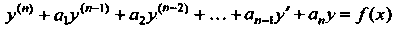(27.12)

И соответствующее ему однородное уравнение

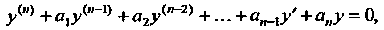(27.13)

У которого коэффициенты те же, что и в уравнении (27.12).

Общее решение уравнения (27.12) определяется формулой

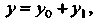(27.14)

Где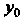- общее решение уравнения (27.13),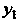- частное решение уравнения (27.12). •

Частное решение уравнения (27.12) можно находить способом вариации произвольных постоянных. В простейших случаях, когда правая часть этого уравнения — алгебраический или тригонометрический многочлен и др., частные решения находят с помощью метода неопределенных коэффициентов:

1. Пусть

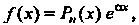(27.15)

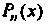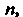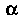Где— многочлен степениЧислоНе является корнем характеристиче

Ского уравнения, тогда

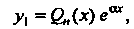(27.16) где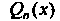- многочлен той же степени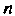С неопределенными коэффициентами;

Если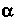- корень кратности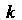Названного уравнения, тогда

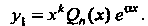
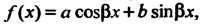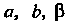2.  ПустьГде- постоянные, и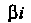Не является корнем характеристического уравнения, тогда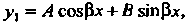Где

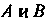
- постоянные неопределенные коэффициенты, и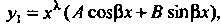Если

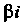- корень кратности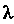Характеристического уравнения.

3.  Пусть

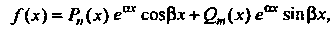
Где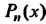И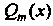— многочлены от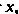Тогда

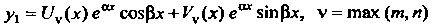
В случае, когда число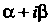Не является корнем характеристического уравнения, и

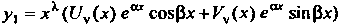
В случае, когда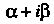- корень кратности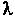Указанного уравнения.

Пример 27.7. Проинтегрировать линейное неоднородное уравне-

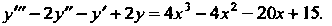
Соответствующее однородное уравнение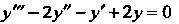Имеет общее

Решение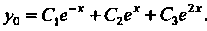

Найдем частное решение исходного уравнения, правая часть которого является многочленом третьей степени (функция (27.15) в случае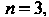

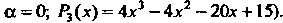В соответствии с формулой (27.16)

Полагаем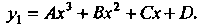Поскольку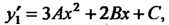

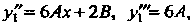То

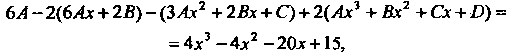
Или

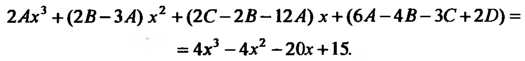
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений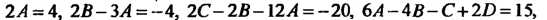

Из которой находимСледовательно,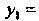

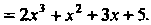По формуле (27.14) получаем общее решение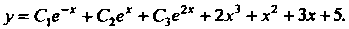

< Предыдущая		Следующая >