27.3. Линейные однородные уравнения л-го порядка с постоянными коэффициентами

Линейным дифференциальным уравнением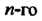Порядка называется уравнение

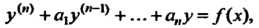
Где коэффициенты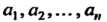- функции от х или постоянные.

Если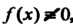, то уравнение называется неоднородным; если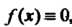, урав

Нение называют однородным, последнее имеет вид

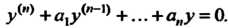(27.8)

Если функции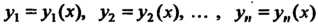Являются линейно неза

Висимыми решениями уравнения (27.8), то его общее решение определяется формулой

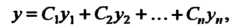(27.9)

Где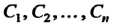- произвольные постоянные.

В случае, когда коэффициенты уравнения (27.8) — постоянные величины, уравнение называется линейным однородным уравнением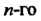Порядка с постоянными коэффициентами. Общее решение его находится так же, как и в случае уравнения второго порядка:

1)  составляется соответствующее характеристическое уравнение

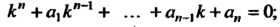
2)  находятся корни характеристического уравнения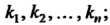

3)  выписываются частные линейно независимые решения, причем принимается во внимание, что:

А)  каждому действительному простому корню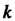Соответствует частное решение;

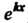Б)  каждой паре комплексно-сопряженных корней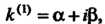

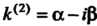Соответствуют два частных решения: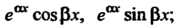

В)  каждому действительному корню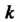Кратности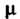Соответствуют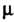Линейно независимых частных решений: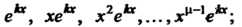

Г)  каждой паре комплексно-сопряженных корней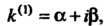

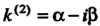Кратности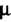Соответствует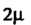Частных решений: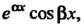

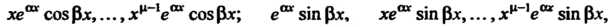
Число частных решений равно степени характеристического уравнения (или порядку данного линейного дифференциального уравнения);

4)  общее решение получается по формуле (27.9), в которой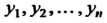-линейно независимые решения.

15 Зак. 1

Тельные числа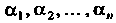, не все равные нулю, такие, что для всех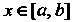

Выполняется тождество

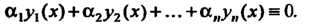(27.11)

-Функции (27.10) называются линейно независимыми, если тождество (27.11) выполняется лишь в случае, когда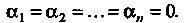

Если функции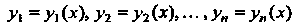Линейно зависимы на от

Резке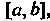То определитель Вронского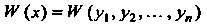Тождественно

Равен нулю на этом отрезке, где

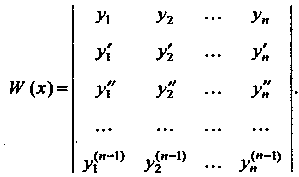
Для линейно независимых функций определитель Вронского не равен нулю ни в одной точке этого отрезка.

Пример 27.3. Проинтегрировать дифференциальное уравнение

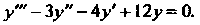
Характеристическое уравнение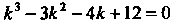Имеет корни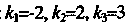

(так как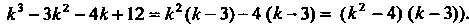Этим корням

Соответствуют линейно независимые решения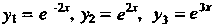. В соот

Ветствии с формулой (27.9) получаем общее решение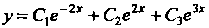

Пример 27.4. Проинтегрировать дифференциальное уравнение

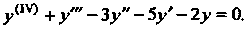
Составляем характеристическое уравнение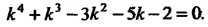Поскольку

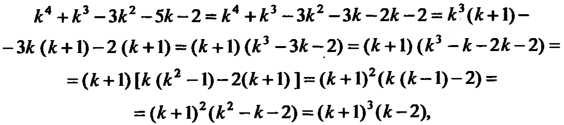
То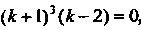, откуда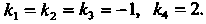

Корень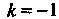Является трехкратным, ему соответствуют линейно незави

Симые решения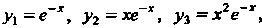, простому корню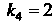Соответ

Ствует решение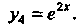Общее решение определяется формулой

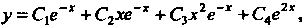Или

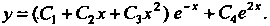
Пример 27.5. Проинтегрировать дифференциальное уравнение

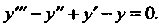
Характеристическое уравнениеИмеет корни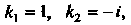

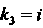(поскольку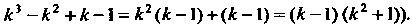Общее* ре

Шение имеет вид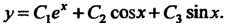

Пример 27.6. Проинтегрировать дифференциальное уравнение

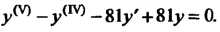
Характеристическое уравнение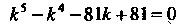Имеет корни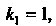

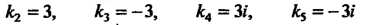(так как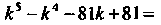

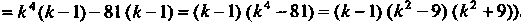Следовательно,

Уравнение имеет общее решение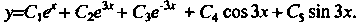

< Предыдущая		Следующая >