27.2. Простейшие интегрируемые дифференциальные уравнения высших порядков

Если дифференциальное уравнение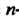-го порядка (27.1) разрешимо относительно старшей производной, то его можно представить в виде

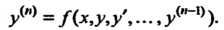(27.5)

Рассмотрим некоторые частные случаи уравнений (27.1) и (27.5). Пусть уравнение (27.1) не содержит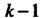Первых последовательных производных, т. е. имеет вид

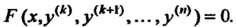(27.6)

Это уравнение подстановкой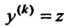Приводится к уравнению

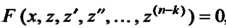, порядок которого равен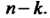

Общее решение уравнения (27.7) находится и-кратным интегрированием. Пример 27.1. Проингефировап. дифференциальное уравнение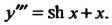 Эго уравнение вида (27.7), его общее решение находится трехкратным интегрированием:

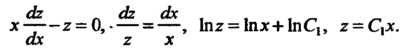
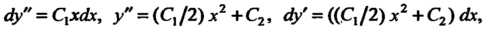
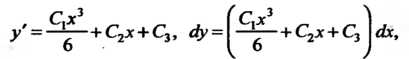
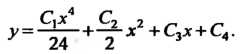
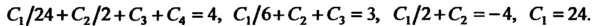
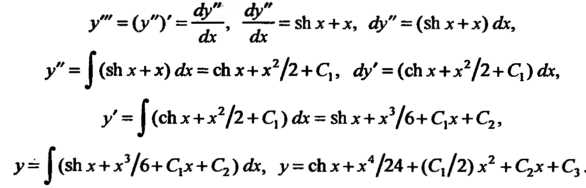
Пример 27.2. Найти решение уравнения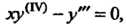Удовлетворяю

Щее условиям: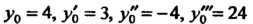При

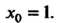
Найдем сначала общее решение данного уравнения, являющееся уравнением вида (27.6). Введем новую переменную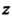По формуле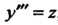, тогда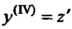

Исходное уравнение примет вид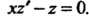Интегрируя это дифференциальное

Уравнение первого порядка, находим

Так как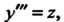То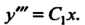Находим общее решение этого уравнения:

Поставляя в выражения для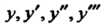Значение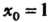И учитывая началь

Ные данные, получаем систему уравнений

Из этой системы определяем значения произвольных постоянных:,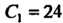

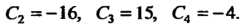Подставив эти значения в формулу (1), найдем искомое частное решение

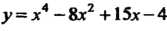
< Предыдущая		Следующая >