27.1. Основные понятия
Дифференциальным уравнением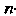
-го порядка называется уравнение, связывающее независимую переменную
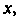Искомую функцию
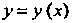И ее производные до порядка п включительно:
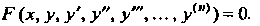(27.1)
Решением дифференциального уравнения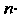
-го порядка называется функция 
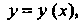Подстановка которой и ее производных в это уравнение обращает его в
Тождество. График решения называется интегральной кривой.
Задача Коши. Найти решение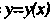
Уравнения (27.1), удовлетворяющее условиям:
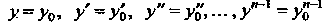При
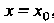, (27.2)
Где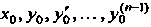
— заданные числа, называемые начальными данными решения.
Теорема 27.1. Если в уравнении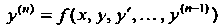
Функция
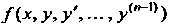И ее частные производные по
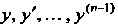Непрерывны в
Некоторой замкнутой области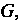
, определяемой неравенствами:
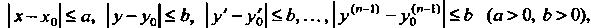
И, следовательно, ограничены в ней, т. е.
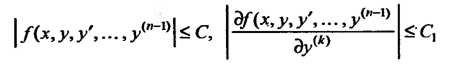
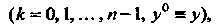
Где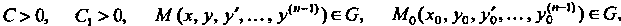
То существует единственное решение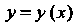
Данного уравнения, удовлетво
Ряющее условиям:
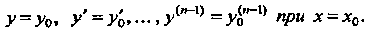
Это решение определено и непрерывно вместе с производными до порядка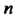
включительно в промежутке
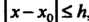, где
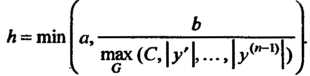
Общим решением дифференциального уравнения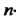
-го порядка (27.1) называется функция
(27.3)
Обладающая следующими свойствами: I) при любых значениях произвольных постоянных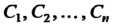
Она обращает уравнение (27.1) в тождество; 2) значения постоянных
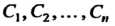Можно подобрать так, чтобы она удовлетворяла условиям (27.2).
Частным решением дифференциального уравнения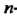
-го порядка называется решение, получающееся из общего решения (27.3) при фиксированных значениях произвольных постоянных, т. е. функция
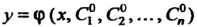, где
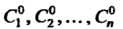- некоторые числа.
Решение дифференциального уравнения и-го порядка, в каждой точке которого нарушается единственность решения задачи Коши, называется особым.
Общим интегралом дифференциального уравнения п-го порядка называется соотношение вида
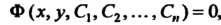(27.4)
Неявно определяющее общее решение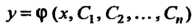
Этого уравнения.
Частным интегралом дифференциального уравнения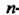
-го порядка называется соотношение
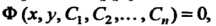Полученное из общего интеграла путем
Фиксирования значений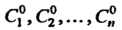
Произвольных постоянных.
| < Предыдущая | Следующая > |
|---|
