27.5. Системы линейных дифференциальных уравнений с постоянными коэффициентами

Системой линейных дифференциальных уравнений с постоянными коэффициентами называется совокупность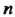Уравнений вида

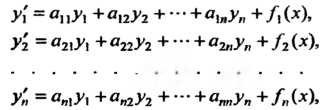(27.17)

Где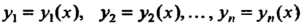— неизвестные функции переменной х,

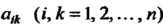— постоянные величины,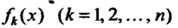- заданные

Функции. Если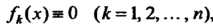, то система называется однородной, в

Противном случае - неоднородной.

Решением системы называется совокупность и функций

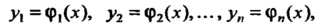
Обращающих каждое из уравнений этой системы в тождество.

Задача Коши. Найти решение системы (27.17), удовлетворяющее условиям:

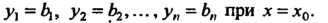
Методом исключения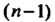Неизвестных функций систему (27.17) в некото

Рых случаях можно привести, к линейному дифференциальному уравнению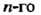 порядка с постоянными коэффициентами относительно одной из функций.

Замечание. Если аргумент функций обозначать через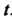, систему (27.17) можно записать так:

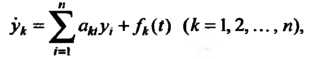(27.18)

Где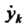- производная функция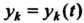По этому аргументу.

Пример 27.8. Найти общее решение системы дифференциальных уравнений с постоянными коэффициентами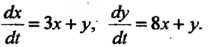 Данную систему запишем в виде

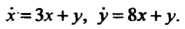
Дифференцируя по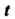Первое уравнение системы и используя данные уравнения, находим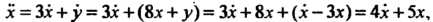

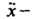
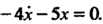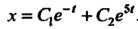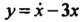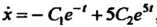Полученное уравнение второго порядка с постоянными коэффициентами имеет обшее решениеПосколькуИ , то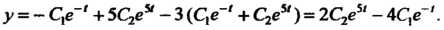

Следовательно, общее решение данной системы определяется формулами

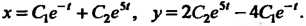
Пример 27.9. Проинтегрировать систему дифференциальных уравнений

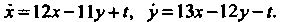
Эта система является неоднородной. Дифференцируя первое уравнение и учитывая данные уравнения, получаем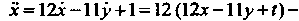

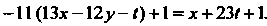Интегрируя неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами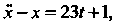Нахо

Дим его общее решениеПоскольку

, то из первого уравнения системы можно найти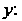

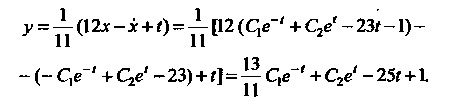
Следовательно, данная система имеет общее решение

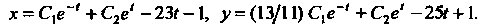
< Предыдущая		Следующая >