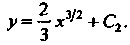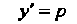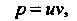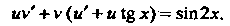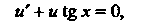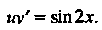26.1. Простейшие дифференциальные уравнения второго порядка. Случаи понижения порядка
Если уравнение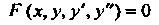 Разрешимо относительно старшей произ
Разрешимо относительно старшей произ
Водной, то его можно представить в виде
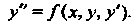 (26.1)
(26.1)
К простейшим интегрируемым дифференциальным уравнениям второго порядка относятся уравнения, для которых функция, стоящая в правой части равенства (26.1), зависит только от одного из трех аргументов:
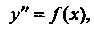 (26.2)
(26.2)
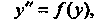 (26.3)
(26.3)
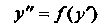 (26.4)
(26.4)
Общее решение уравнения (26.2) находится двукратным интегрированием.
Которая дает возможность свести их к уравнениям с разделяющимися переменными: 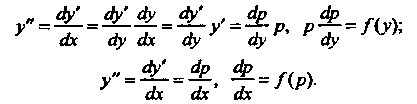 Уравнение
Уравнение
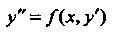 (26.6)
(26.6)
Подстановкой (26.5) приводится к уравнению первого порядка
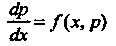
С неизвестной функцией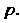 Уравнение
Уравнение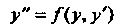
Той же подстановкой сводится к уравнению первого порядка
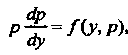
В котором роль независимой переменной играет у.
Пример 26.1. Проинтегрировать дифференциальное уравнение
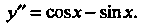
Это уравнение вида (26.2). Преобразуя исходное уравнение, получаем
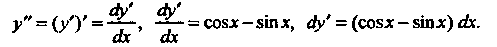
Интегрируя последнее уравнение, находим производную искомой функции 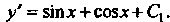 Так как
Так как
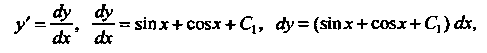
То в результате интегрирования полученного уравнения нахСдим общее решение
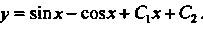
Пр имер 26.2. Найти частное решение дифференциального уравнения 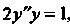 , удовлетворяющее условиям:
, удовлетворяющее условиям: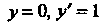 При
При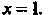
Данное уравнение можно разрешить относительно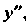 , правая часть его будет зависеть только от у, это уравнение вида (26.4).
, правая часть его будет зависеть только от у, это уравнение вида (26.4).
Применяем подстановку (26.5), т. е. полагаем Тогда
Тогда
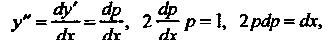
Откуда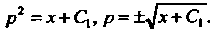 Из начального условия
Из начального условия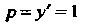 При
При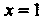
Используя начальное условие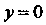 При
При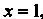 J определяем
J определяем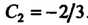 . Функция (1)
. Функция (1)
Принимает вид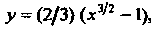 , она определяет искомое частное решение.
, она определяет искомое частное решение.
Пример 26.3. Найти общее решение дифференциального уравнения
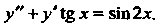
Это уравнение вида (26.6). Применяем подстановку (26.5). Так как
И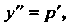 То исходное уравнение можно записать так:
То исходное уравнение можно записать так:
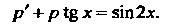
Уравнение (2) является линейным дифференциальным уравнением первого порядка относительно неизвестной функции р. Полагая
Находим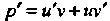 И подставляем выражения для
И подставляем выражения для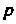 И
И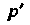 В уравнение (2):
В уравнение (2):
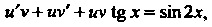
В качестве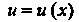 Возьмем функцию, для которой
Возьмем функцию, для которой
Тогда уравнение (4) примет вид
Из уравнения (5) находим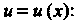
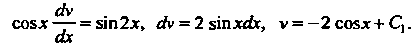
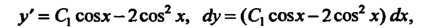
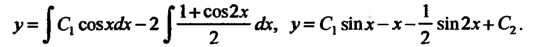
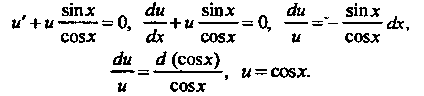
Подставив это выражение в уравнение (6), получим
По формуле (3) найдем Уравнение (1) примет вид
Уравнение (1) примет вид
Откуда
| < Предыдущая | Следующая > |
|---|