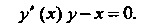25.5. Задачи, приводящие к дифференциальным уравнениям

Решение многих научных и технических задач приводит к интегрированию дифференциальных уравнений. В этих задачах требуется установить зависимость между переменными величинами некоторого физического, химического или другого процесса, найти уравнение линии или поверхности и т. п.

При решении таких задач можно руководствоваться следующим.

1.  Необходимо сначала составить дифференциальное уравнение из условия задачи.

2.  Определить тип полученного уравнения и выбрать метод решения.

3.  Найти общее решение уравнения.

4.  Получить частное решение, удовлетворяющее данным начальным условиям.

5.  В случае необходимости вычислить значения вспомогательных параметров (коэффициент пропорциональности и др.).

6.  Бели это требуется, найти численные значения искомых величин.

Составление дифференциального уравнения по условию научной или технической задачи состоит в определении математической зависимости между переменными величинами и их приращениями, в нахождении выражения для производной.

В некоторых случаях приращения целесообразно сразу заменить соответствующими дифференциалами.

При составлении дифференциальных уравнений используются соответственно геометрический или механический смысл производной; кроме того, в зависимости

От условия задачи применяются соответствующие законы физики, механики, химии и других наук.

Пр имер 25.5. Найти линию, у которой отрезок нормали в любой ее точке, заключенный между осями координат, делится пополам в этой точке. Составить уравнение такой линии, проходящей через точку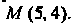

Пусть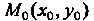- произвольная точка

(рис. 25.1) искомой линии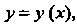Где-

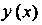Пока неизвестная функция аргумента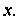Уравне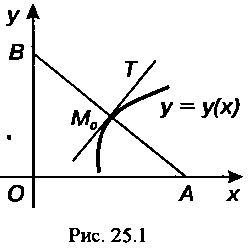Ние нормали к линии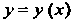В точке

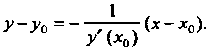
Обозначим через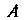И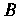Точки пересечения нормали с координатными осями. Положив в этом уравнении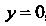, найдем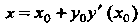- абсциссу точки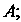

При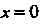Из того же уравнения найдем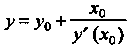— ординату точки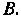

Поскольку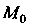— середина отрезка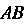, то

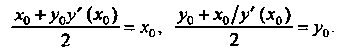
Каждое из этих уравнений приводится к уравнению

(1)

Уравнению (1) удовлетворяют координаты любой точки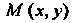Искомой

Линии, поэтому

(2)

Уравнение (2) является уравнением с разделяющимися переменными. Разделяя переменные и интегрируя, получаем общий интеграл

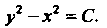
Общий интеграл (3) определяет множество равносторонних гипербол с действительной осью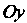При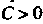; множество равносторонних гипербол с действительно осью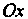ПриПару прямых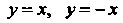При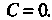Найдем ту линию, которая проходит через точку М (5,4). Подставив в уравнение (3) координаты точки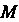, определим значение параметра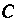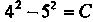,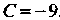. При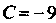 уравнение (3) принимает вид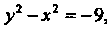, или

Гпава 26

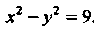
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА

Дифференциальным уравнением второго порядка называется уравнение относительно искомой функции, ее первой и второй производной. В общем виде это уравнение можно записать так:

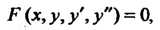
Где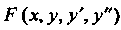- заданная функция указанных аргументов.

Общим решением дифференциального уравнения второго порядка называется функция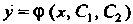От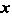И двух независимых произвольных постоянных

И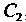, обращающая данное уравнение в тождество. Общее решение, заданное в неявном виде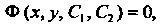Называют общим интегралом.

Частным решением уравнения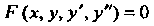Называется решение

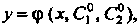Получающееся из общего путем фиксирования значений произвольных постоянных: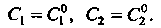

Задача Коши. Найти решение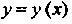Дифференциального уравнения второго по

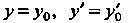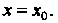Рядка, удовлетворяющее условиям:ПриЧисла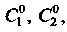Опреде

Ляющие искомое частное решение, находятся из системы уравнений:

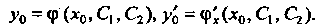
< Предыдущая		Следующая >