25.2. Однородные уравнения
Функция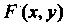 Называется однородной измерения т, если для любых t
Называется однородной измерения т, если для любых t
Выполняется тождество
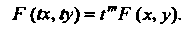 (25.2)
(25.2)
Дифференциальное уравнение первого порядка
 (25.3)
(25.3)
Называется однородным, если — однородные функции одного
— однородные функции одного
И того же измерения.
С помощью новой переменной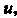 Вводимой по формуле
Вводимой по формуле
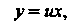 (25.4)
(25.4)
Однородное уравнение приводится к уравнению с разделяющимися переменными. Уравнение
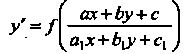 (25.5)
(25.5)
Также можно привести к однородному уравнению с помощью преобразования 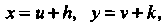 Где
Где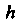 И
И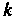 Определяются системой уравнений
Определяются системой уравнений
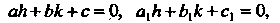
В случае, когда
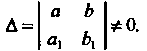
Уравнение (25.5) сводится к уравнению с разделяющимися переменными с помощью преобразования В случае, когда
В случае, когда
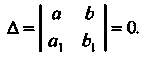
Пример 25.2. Найти общее решение дифференциального уравнения
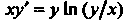
Это уравнение приводится к виду (25.3), где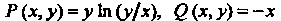
- однородные функции первого измерения; они удовлетворяют условию (25.2) при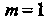 . Полагая
. Полагая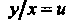 , или
, или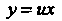 (см. (25.4)), находим
(см. (25.4)), находим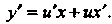 Под
Под
Ставляя эти выражения в исходное уравнение, получаем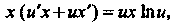
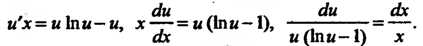
Вводя новую переменную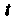 По формуле
По формуле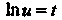 И интегрируя, находим
И интегрируя, находим
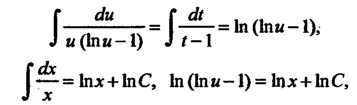
Откуда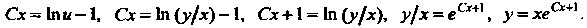
Следовательно, - общее решение.
- общее решение.
| < Предыдущая | Следующая > |
|---|