25.3. Линейные уравнения. Уравнение Бернулли
Уравнение
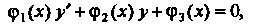
Или
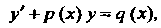 (25.6)
(25.6)
Называется линейным дифференциальным уравнением первого порядка.
Решение линейного уравнения ищут в виде произведения двух функций:
Подстановка выражений для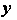 И
И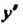 В уравнение (25.6) приводит его к виду
В уравнение (25.6) приводит его к виду
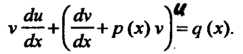
В качестве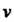 Выбирают одну из функций, удовлетворяющих уравнению
Выбирают одну из функций, удовлетворяющих уравнению 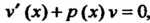 Тогда функция и определяется уравнением
Тогда функция и определяется уравнением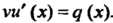
Для решения уравнения (25.6) можно применить метод вариации произвольной постоянной, состоящий в следующем: сначала находят общее решение соответствующего однородного уравнения (т. е. уравнения, для которого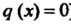 ); величину
); величину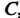 , входящую в это общее решение, полагают функцией х и находят ее. Уравнением Бернулли называется уравнение
, входящую в это общее решение, полагают функцией х и находят ее. Уравнением Бернулли называется уравнение
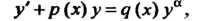
Где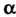 - действительное число. Это уравнение является линейным в случае
- действительное число. Это уравнение является линейным в случае 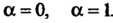 В других случаях оно сводится к линейному с, помощью
В других случаях оно сводится к линейному с, помощью
Подстановки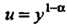
Пример 25.3. Проинтегрировать дифференциальное уравнение
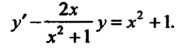
Данное уравнение является линейным. Решение этого уравнения ищем в виде (25.7). Поскольку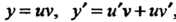 , то
, то
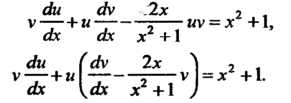
В качестве v выберем одну из функций, обращающих в нуль коэффициент при и в уравнении (1), т. е. решение уравнения
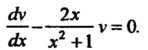
Уравнение (2) является уравнением с разделяющимися переменными И
И Разделив переменные, получим
Разделив переменные, получим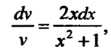
Откуда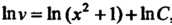
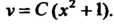
Полагая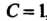 , получаем
, получаем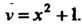 Уравнение (1) с учетом (2) сводится к
Уравнение (1) с учетом (2) сводится к
Уравнению
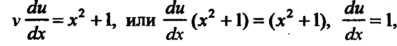
Из которого определяется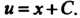 По формуле (25.7) находим общее решение
По формуле (25.7) находим общее решение 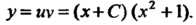
| < Предыдущая | Следующая > |
|---|