25.1. Уравнение с разделяющимися переменными

Дифференциальным уравнение первого порядка с разделяющимися переменными называется уравнение вида

Где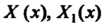- функции только от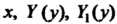- функции только от.

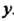Предположив, что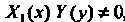, и разделив обе части уравнения (2S.1) на

Это произведение, получим уравнение

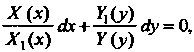
Которое называют уравнением с разделенными переменными; оно имеет общий интеграл

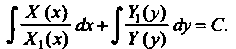
Замечание. Корни уравнений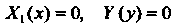Являются реше

Ниями уравнения (2S. 1).

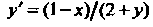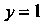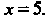Пример 2S.1. Проинтегрировать дифференциальное уравнение . Найти решение, удовлетворяющее условиюПри Это уравнение можно записать в виде

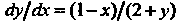, или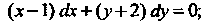

Интегрируя, получаем

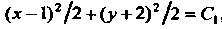, или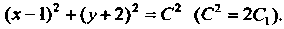

Общий интеграл данного уравнения геометрически представляет собой множество концентрических окружностей с центром в точке S (1,-2). Найдем решение, удовлетворяющее указанному условию. Подставив в выражение для общего интеграла значения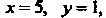Определим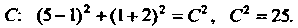Следовательно, искомый частный интеграл имеет ввд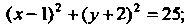Он определяет окружность, проходящую через точку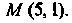

< Предыдущая		Следующая >