24.7. Степенные ряды с комплексной переменной

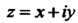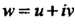Рассмотрим две комплексные переменные величиныИ, где

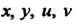- действительные переменные,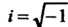- мнимая единица. Если каж

Дому значению переменной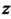Из некоторого множества соответствует единственное значение переменной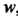, то говорят, что w есть функция от:

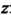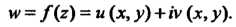
Здесь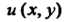И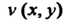- действительные функции от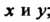Задание одной

Функции от одной комплексной переменной означает задание двух действительных функций от двух действительных переменных.

Комплексным функциональным рядом называется ряд

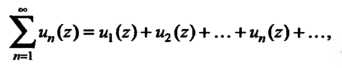(24.32)

Члены которого являются функциями комплексной переменной.

Значения z, при которых ряд (24.32) сходится, называются точками сходимости. Множество всех точек сходимости называется областью сходимости этого ряда. Для каждого числа z из области сходимости

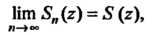
Где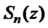. - частная сумма ряда (24.32), а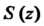- его сумма.

Ряд (24.32) сходится, если сходится ряд из модулей его членов.

Степенным рядом с комплексными членами называется ряд вида

(24.33)

Где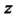- комплексная переменная,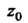- данное комплексное число, коэффициенты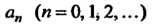- данные комплексные числа.

В частном случае, при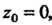Получаем комплексный степенной ряд, располо-

Жейный по степеням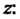

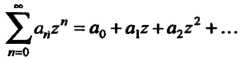(24.34)

Для каждогостепенного ряда (24.33) существует круг радиуса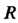С центром в точке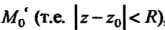, внутри которого данный ряд сходится, а вне его расхо

Дится (т. е. при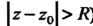|. Этот круг называется кругом сходимости. Его радиус

Называется радиусом сходимости степенного ряда (, если степенной ряд сходится во всей плоскости,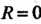, если он сходится лишь в центре круга, в точке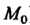). Во всех точках внутри круга сходимости степенной ряд абсолютно сходится.

При отыскании радиуса сходимости степенного ряда могут применяться признаки сходимости Д’Аламбера и Коши. В частности, радиус сходимости степенного ряда (24.33) можно вычислить по формуле

(24.35)

Показательная и тригонометрические функции комплексной переменной определяются формулами

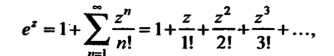(24.36)

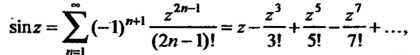(24.37)

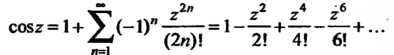(24.38)

Ряды в правых частях формул (24.36) - (24.38) сходятся при всех комплексных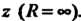

Связь между этими функциями устанавливают формулы Эйлера:

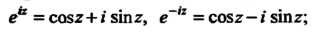
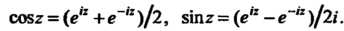(24.39)

Отметим, что

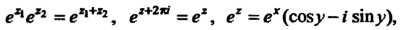(24.40)

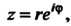(24.41)

Где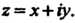

Вторая из формул (24.40) означает, что функция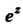Имеет период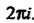, Формула (24.41) представляет комплексное число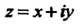В показательной форме (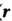-модуль,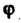- аргумент).

Пример 24.25. Найти область сходимости рядаи его сумму.

Составим ряд из модулей членов данного ряда: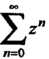

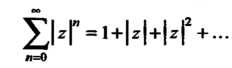
Полученный ряд является рядом с действительными членами, он представляет собой геометрический ряд. Следовательно, этот ряд сходится, когда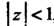, т. е. в круге радиуса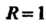С центром в начале координат. Таким образом, данный ряд также сходится в круге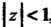, который и является его областью сходимости.

Так как частная сумма ряда выражается формулой

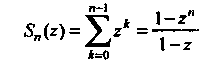
И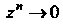При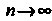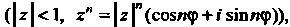То сумма ряда

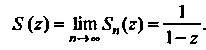
Итак, получено следующее разложение:

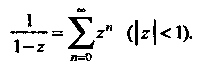
Пример 24.26. Найти область сходимости ряда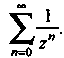 Рассмотрим ряд, составленный из модулей членов данного ряда

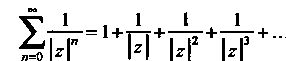
Этот ряд является геометрическим. Так как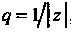, то ряд сходится при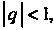

Т. е. при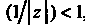, или при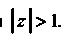

Итак, областью сходимости является множество точек, лежащих вне круга радиуса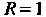С центром в начале координат.

Пример 24.27. Найти радиус сходимости степенного ряда

Поскольку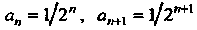, то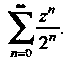

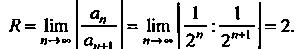
Итак, радиус сходимости данного ряда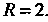

Пример 24.28. Найти область сходимости ряда Поскольку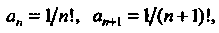То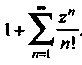

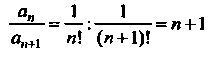
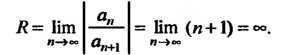
Данный ряд сходится на всей комплексной плоскости.

Пример 24.29. Найти сумму

Используя третью го формул (24.39), получаем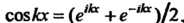, поэтому

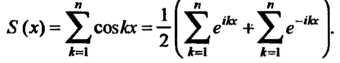
Суммируя геометрические прогрессии, находим

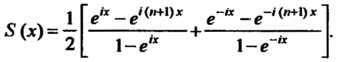
Разделив почленно первую дробь на, вторую на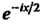, получим

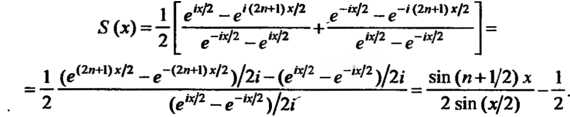
Итак,

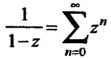
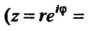
Пример 24.30. С помощью разложения 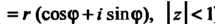) получить следующие:

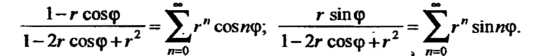
Первое разложение получено в пример 24.25. Подставив в него выражение 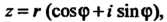Найдем

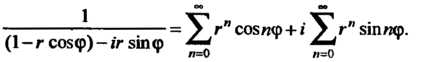
Преобразуем левую часть данного равенства:

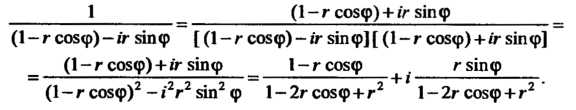
Следовательно,

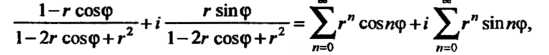
Откуда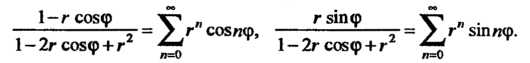

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Дифференциальным уравнением называется уравнение относительно неизвестной функции и ее производных различных порядков. Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение.

Если искомая функция зависит от одной переменной, то соответствующее дифференциальное уравнение называется обыкновенным. Если искомая функция зависит от нескольких переменных, то соответствующее дифференциальное уравнения называется уравнением с частными производными. В главах 25 и 27 рассматриваются обыкновенные дифференциальные уравнения.

Обыкновенное дифференциальное уравнение п-го порядка в общем визе можно записать так:

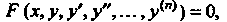
Где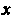- независимая переменная;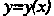- искомая функция переменной 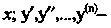ее производные;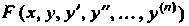- заданная функция своих аргументов.

Отметим, что функция F может не содержать некоторых своих аргументов, но непременно должна зависеть от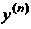(когца речь идет об уравнении и-го порядка).

Если данное уравнение разрешимо относительно производной п-го порядка, его можно представить в виде

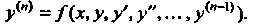
Функция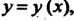Определенная и непрерывно дифференцируемая п раз в ин

Тервале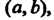Называется решением дифференциального уравнения в этом ин

Тервале, если она обращает данное уравнение в тождество, т. е.

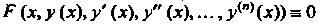
Для всех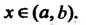

График решения дифференциального уравнения п-то порядка называется интегральной линией (или интегральной кривой).

Термин «дифференциальное уравнение» принадлежит Лейбницу (1676, опубликовано в 1684 г.). Начало исследований по дифференциальным уравнениям восходит ко временам Лейбница, Ньютона, в работах которых исследовались первые задачи, приводящие к таким уравнениям. Лейбниц, Ньютон, братья Я. и И. Бернулли разрабатывали методы интегрирования обыкновенных дифференциальных уравнений. В качестве универсального способа использовались разложения интегралов дифференциальных уравнений в степенные ряды. Некоторые классы уравнений были приведены к к уравнению с разделяющимися переменными.

Возникновение теории дифференциальных уравнений в частных производных было связано с расширением в XVIII в. области приложений математического анали - ) за. Оно стимул ировалось теми задачами естествознания, механики, физики, в которых появилась необходимость в функциях нескольких переменных.

Первые примеры интегрирования уравнений с частными производными даны в работах Эйлера (1734). Теорию уравнений с частными производными интенсивно развивали Эйлер, Д'Аламбер, Д. Бернулли,. Новые иаеи в этой области в конце XVIII в. предложены в сочинениях Лагранжа, Лапласа, Монжа.

В 1807 г. Фурье вывел уравнение теплопроводности и для его решения разработал метод разделения переменных, названный его именем. Решением задач, возникавших в теории теплопроводности занимались многие математики, в том числе Гаусс, Пуассон, Грин, М. В. Остроградский и др.

Глава 25

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную, искомую функцию этой переменной и ее производную. Если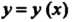- функция независимой переменной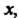То в общем

Виде уравнение записывается так:

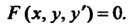
Если это уравнение разрешимо относительн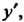оТо

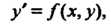
Откуда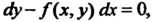Или в более общем виде

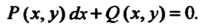
Решением дифференциального уравнения называется всякая функция 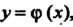, обращающая уравнение в тождество. В случае, если эта функция задана в неявном виде, решение называют интегралом. График решения дифференциального уравнения называется интегральной кривой.

Общим решением дифференциального уравнения первого порядка называется функция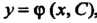, где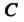— произвольная постоянная, - обращающая данное

Уравнение в тождество.

Общее решение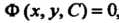, заданное в неявном виде, называется общим

Интегралом этого уравнения.

Геометрически общее решение (и общий интеграл) представляет собой семейство интегральных кривых на плоскости, зависящее от одного параметра С.

Частным решением уравнения называется решение, полученное из общего решения при фиксированном значении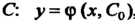, где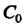- число. Аналогично определяется частный интеграл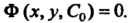

Задача Коши. Найти решение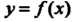Дифференциального уравнения первого

Порядка, удовлетворяющее начальному условию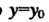При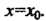Другими словами, найти интегральную кривую этого уравнения, проходящую через точку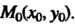

< Предыдущая		Следующая >