24.6. Ряды Фурье

Г

Рядом Фурье функцииНазывается тригонометрический ряд

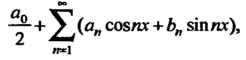(24.25)

Коэффициенты которого определяются формулами

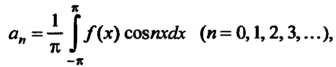(24.26)

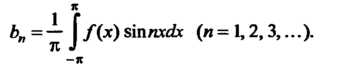(24.27)

Ряды Фурье периодаЕсли функция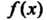С периодом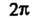Кусочно

Дифференцируема в промежутке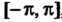, то ее ряд Фурье сходится в любой точке

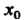И имеет сумму

В частности, в точке непрерывности функции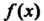Сумма ее ряда Фурье равна значению самой, функции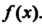На концах промежутка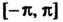Имеем

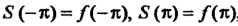, если функция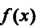Непрерывна в точках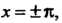И

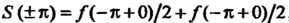, если она разрывна в этих точках.

Ряд Фурье четной функции содержит только члены с косинусами; ряд Фурье нечетной функции содержит только члены с синусами.

Кусочно-дифференцируемая функция, заданная на полупериоде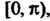Может

Быть продолжена в промежуток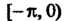Либо как четная, либо как нечетная, в

Соответствии с чем ее можно разложить в ряд Фурье или только по косинусам, или только по синусам кратныхдуг.

Ряды Фурье периода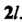, Если функция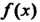И ее производная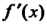В проме

Жутке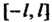Либо непрерывны, либо имеют лишь конечное число точек разрыва пер

Вого рода, то во всех точках непрерывности этого промежутка справедливо разложение

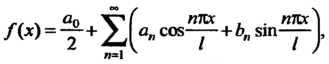(24.29)

Где

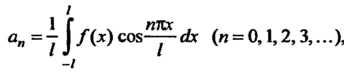(24.30)

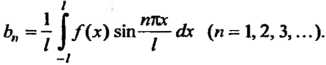(24.31)

В точках разрыва функции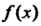И на концах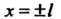Промежутк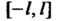аСумма

Ряда Фурье определяется формулой (24.28).

В случае разложения функции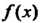В ряд Фурье в произвольном промежутке 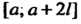Длины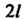Пределы интегрирования в формулах (24.30), (24.31) следует

Заменить соответственно через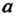И

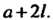
Ряд Фурье (24.25) можно представить в комплексной форме

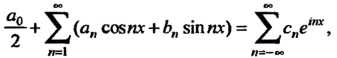
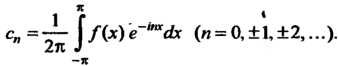
Аналогично представляется в комплексной форме и ряд Фурье в правой части формулы (24.29).

Пример 24.21. В промежуткеРазложить в ряд Фурье

Функцию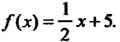

По формулам (24.26), (24.27) находим коэффициенты

Следовательно,

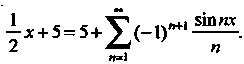
Пример 24.22. Разложить в ряд Фурье функцию 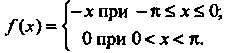 С помощью полученного разложения показать, что

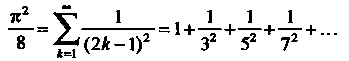
По формулам (24.26) и (24.27) находим коэффициенты ряда Фурье: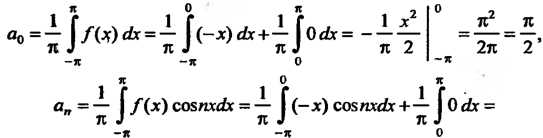

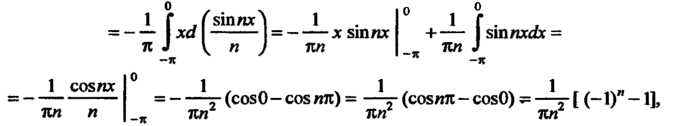
Т. е.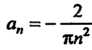• при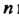Нечетном,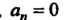При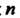Четном;

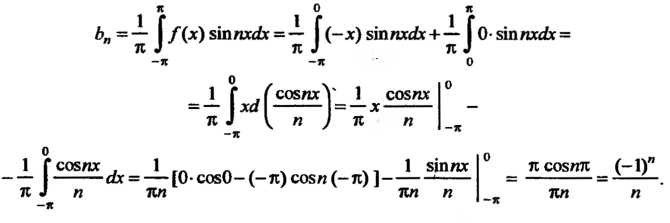
Таким образом,

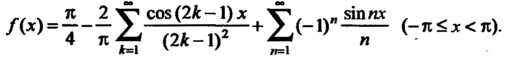
При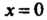Получаем

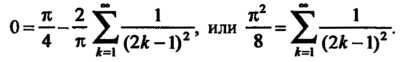
Пример 24.23. Функцию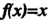В промежутке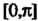Разложить по косинусам.

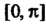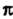В. данном случае требуется получить разложение функции в промежутке длины(а не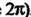,. Продолжая функцию в промежуток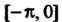Четным образом, заклю

Чаем, что ее разложение в ряд Фурье содержит только косинусы, т. е. все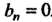. Коэффициенты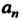Находим по формулам, получающимся из формул (24.26) для этого случая: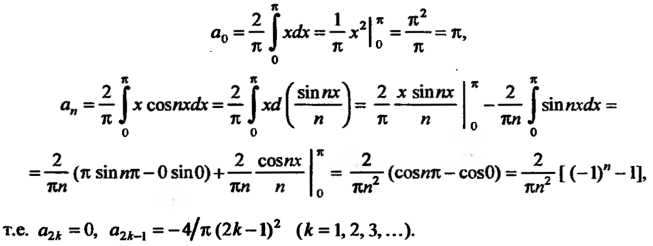

Следовательно,

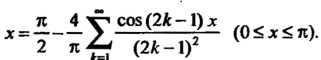
Пример 24.24. Разложить в ряд Фурье функцию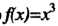В промежутке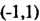

Данная функция является нечетной, поэтому разложение (24.29) будет содержать только члены с синусами, все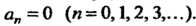Коэффициенты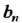В этом случае можно определять по формуле

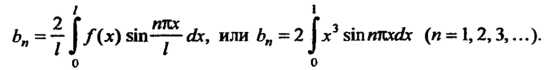
Найдем эти коэффициенты:

Следовательно, при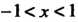Получаем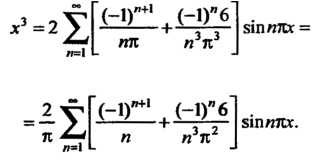

< Предыдущая		Следующая >