24.5. Применения рядов в приближенных вычислениях
С помощью рядов можно вычислить значения тригономегричеких функций, логарифмов чисел, корней, определенных интегралов.
Значения тригонометрических функций (синуса и косинуса) можно вычислить с помощью их разложений в степенные ряды.
Для вычисления натуральных логарифмов чисел применяется формула
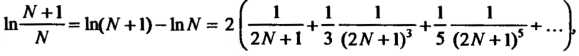(24.23)
Которая получается из формулы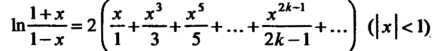 
при
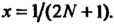
Погрешность при замене суммы ряда (24.23) суммой его и первых членов определяется формулой
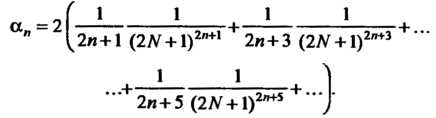
Очевидно,
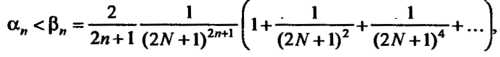
Или
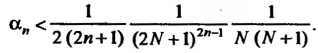
Для вычисления корней применяют биномиальный ряд, т. е. степенной ряд для функции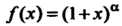
. Предположим, что нужно вычислить
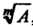, причем уже
Известно приближенное значение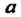
Этого корня, но требуется улучшить его. Если 
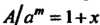, где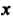
- небольшая правильная дробь, то можно преобразовать корень следующим образом:
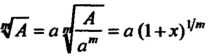(24.24)
И применить биномиальный ряд при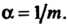
Если подынтегральная функция разлагается в степенной ряд, а пределы интегрирования принадлежат области сходимости этого ряда, соответствующий определенный интеграл можно вычислить приближенно.
Пример 24.20. Вычислить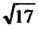
С точностью до 0,0001.
Преобразование (23.24) в данном случае принимает вид
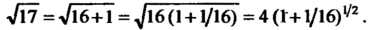
Воспользуемся биномиальным рядом. Полагая в нем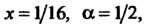
Получаем
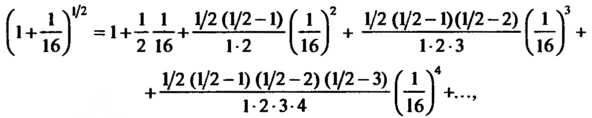
Т. е.
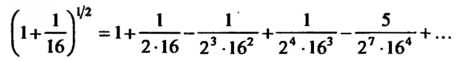
Полученный ряд (если не принимать во внимание первый член) является знакочередующимся рядом, удовлетворяющим условиям признака Лейбница. Погрешность при вычислении его суммы не превышает первого отброшенного члена. Так как
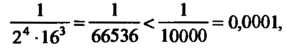
То достаточно взять сумму первых трех членов ряда, чтобы получить искомое значение корня с заданной точностью: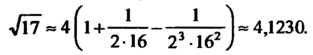
| < Предыдущая | Следующая > |
|---|
